有理数2,1, ,0中,最小的数是
| A. |
2 |
B. |
1 |
C. |
|
D. |
0 |
如图,直线 , 被直线 所截, , ,则 的度数是

| A. |
|
B. |
|
C. |
|
D. |
|
下列调查中,最适宜采用全面调查(普查)的是
| A. |
调查一批灯泡的使用寿命 |
| B. |
调查漓江流域水质情况 |
| C. |
调查桂林电视台某栏目的收视率 |
| D. |
调查全班同学的身高 |
下面四个几何体中,左视图为圆的是
| A. |
|
B. |
|
C. |
|
D. |
|
若 ,则 的值是
| A. |
|
B. |
0 |
C. |
1 |
D. |
2 |
因式分解 的结果是
| A. |
|
B. |
|
C. |
|
D. |
|
下列计算正确的是
| A. |
|
B. |
|
C. |
|
D. |
|
直线 过点 ,则 的值是
| A. |
|
B. |
|
C. |
1 |
D. |
2 |
不等式组 的整数解共有
| A. |
1个 |
B. |
2个 |
C. |
3个 |
D. |
4个 |
如图, 是 的弦, 与 相切于点 ,连接 , ,若 ,则 的度数是

| A. |
|
B. |
|
C. |
|
D. |
|
参加足球联赛的每两支球队之间都要进行两场比赛,共要比赛110场,设参加比赛的球队有 支,根据题意,下面列出的方程正确的是
| A. |
|
B. |
|
C. |
|
D. |
|
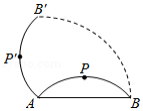
如图,已知 的半径为5,所对的弦 长为8,点 是 的中点,将 绕点 逆时针旋转 后得到 ,则在该旋转过程中,点 的运动路径长是
| A. |
|
B. |
|
C. |
|
D. |
|
2020的相反数是 .
计算: .
如图,在中,,,,则的值是 .

一个正方体的平面展开图如图所示,任选该正方体的一面出现“我”字的概率是 .

反比例函数的图象如图所示,下列关于该函数图象的四个结论:①;②当时,随的增大而增大;③该函数图象关于直线对称;④若点在该反比例函数图象上,则点也在该函数的图象上.其中正确结论的个数有 个.

如图,在中,,点,分别是,的中点,点是扇形的上任意一点,连接,,则的最小值是 .

计算:.
解二元一次方程组:.
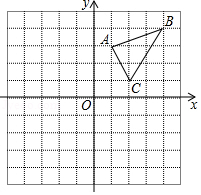
如图,在平面直角坐标系中,的三个顶点分别是,,.
(1)把向左平移4个单位后得到对应的△,请画出平移后的△;
(2)把绕原点旋转后得到对应的△,请画出旋转后的△;
(3)观察图形可知,△与△关于点 , 中心对称.
阅读下列材料,完成解答:
材料1:国家统计局2月28日发布了2019年国民经济和社会发展统计公报,该公报中的如图发布的是全国“年快递业务量及其增长速度”统计图(如图.

材料月28日,国家邮政局发布的数据显示:受新冠疫情影响,快递业务量快速增长,5月份快递业务量同比增长(如图.某快递业务部门负责人据此估计,2020年全国快递业务量将比2019年增长.

(1)2018年,全国快递业务量是 亿件,比2017年增长了 ;
(2)年,全国快递业务量增长速度的中位数是 ;
(3)统计公报发布后,有人认为,图1中表示年增长速度的折线逐年下降,说明年全国快递业务量增长速度逐年放缓,所以快递业务量也逐年减少.你赞同这种说法吗?为什么?
(4)若2020年全国快递业务量比2019年增长,请列式计算2020年的快递业务量.
如图,在菱形中,点,分别是边,的中点.
(1)求证:;
(2)若,,求菱形的面积.

某学校为丰富同学们的课余生活,购买了一批数量相等的象棋和围棋供兴趣小组使用,其中购买象棋用了420元,购买围棋用了756元,已知每副围棋比每副象棋贵8元.
(1)求每副围棋和象棋各是多少元?
(2)若该校决定再次购买同种围棋和象棋共40副,且再次购买的费用不超过600元,则该校最多可再购买多少副围棋?
如图,已知抛物线过点,交轴于点和点(点在点的左侧),抛物线的顶点为,对称轴交轴于点,连接.
(1)直接写出的值,点的坐标和抛物线对称轴的表达式;
(2)若点是抛物线对称轴上的点,当是等腰三角形时,求点的坐标;
(3)点是抛物线上的动点,连接,,将沿所在的直线对折,点落在坐标平面内的点处.求当点恰好落在直线上时点的横坐标.
