下列实数是无理数的是
| A. |
|
B. |
1 |
C. |
0 |
D. |
|
下列图形是中心对称图形的是
| A. |
|
B. |
|
C. |
|
D. |
|
2020年2月至5月,由广西教育厅主办,南宁市教育局承办的广西中小学"空中课堂"是同期全国服务中小学学科最齐、学段最全、上线最早的线上学习课程,深受广大师生欢迎.其中某节数学课的点击观看次数约889000次,则数据889000用科学记数法表示为
| A. |
|
B. |
|
C. |
|
D. |
|
下列运算正确的是
| A. |
|
B. |
|
C. |
|
D. |
|
以下调查中,最适合采用全面调查的是
| A. |
检测长征运载火箭的零部件质量情况 |
| B. |
了解全国中小学生课外阅读情况 |
| C. |
调查某批次汽车的抗撞击能力 |
| D. |
检测某城市的空气质量 |
一元二次方程 的根的情况是
| A. |
有两个不等的实数根 |
B. |
有两个相等的实数根 |
| C. |
无实数根 |
D. |
无法确定 |
如图,在 中, , ,观察图中尺规作图的痕迹,则 的度数为
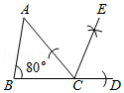
| A. |
|
B. |
|
C. |
|
D. |
|
一只蚂蚁在如图所示的树枝上寻觅食物,假定蚂蚁在每个岔路口都随机选择一条路径,则它获得食物的概率是

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在 中, ,高 ,正方形 一边在 上,点 , 分别在 , 上, 交 于点 ,则 的长为

| A. |
15 |
B. |
20 |
C. |
25 |
D. |
30 |
甲、乙两地相距 ,提速前动车的速度为 ,提速后动车的速度是提速前的1.2倍,提速后行车时间比提速前减少 ,则可列方程为
| A. |
|
B. |
|
| C. |
|
D. |
|
《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图1、2(图2为图1的平面示意图),推开双门,双门间隙 的距离为2寸,点 和点 距离门槛 都为1尺 尺 寸),则 的长是

| A. |
50.5寸 |
B. |
52寸 |
C. |
101寸 |
D. |
104寸 |
如图,点 , 是直线 上的两点,过 , 两点分别作 轴的平行线交双曲线 于点 , .若 ,则 的值为

| A. |
5 |
B. |
|
C. |
4 |
D. |
|
如图,在数轴上表示的的取值范围是 .

计算: .
某射击运动员在同一条件下的射击成绩记录如下:
射击次数 |
20 |
40 |
100 |
200 |
400 |
1000 |
“射中9环以上”的次数 |
15 |
33 |
78 |
158 |
321 |
801 |
“射中9环以上”的频率 (结果保留小数点后两位) |
0.75 |
0.83 |
0.78 |
0.79 |
0.80 |
0.80 |
根据频率的稳定性,估计这名运动员射击一次时“射中9环以上”的概率是 0.8 (结果保留小数点后一位).
如图,某校礼堂的座位分为四个区域,前区一共有8排,其中第1排共有20个座位(含左、右区域),往后每排增加两个座位,前区最后一排与后区各排的座位数相同,后区一共有10排,则该礼堂的座位总数是 .

以原点为中心,把点 逆时针旋转得到点,则点的坐标为 .
如图,在边长为的菱形中,,点,分别是,上的动点,且,与交于点.当点从点运动到点时,则点的运动路径长为 .
计算:.
先化简,再求值:,其中.
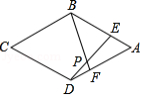
如图,点,,,在一条直线上,,,.
(1)求证:;
(2)连接,求证:四边形是平行四边形.

小手拉大手,共创文明城.某校为了了解家长对南宁市创建全国文明城市相关知识的知晓情况,通过发放问卷进行测评,从中随机抽取20份答卷,并统计成绩(成绩得分用表示,单位:分),收集数据如下:
90 82 99 86 98 96 90 100 89 83 87 88 81 90 93 100 100 96 92 100
整理数据:
3 |
4 |
8 |
分析数据:
平均分 |
中位数 |
众数 |
92 |
根据以上信息,解答下列问题:
(1)直接写出上述表格中,,的值;
(2)该校有1600名家长参加了此次问卷测评活动,请估计成绩不低于90分的人数是多少?
(3)请从中位数和众数中选择一个量,结合本题解释它的意义.
如图,一艘渔船位于小岛的北偏东方向,距离小岛的点处,它沿着点的南偏东的方向航行.
(1)渔船航行多远距离小岛最近(结果保留根号)?
(2)渔船到达距离小岛最近点后,按原航向继续航行到点处时突然发生事故,渔船马上向小岛上的救援队求救,问救援队从处出发沿着哪个方向航行到达事故地点航程最短,最短航程是多少(结果保留根号)?

倡导垃圾分类,共享绿色生活.为了对回收的垃圾进行更精准的分类,某机器人公司研发出型和型两款垃圾分拣机器人,已知2台型机器人和5台型机器人同时工作共分拣垃圾3.6吨,3台型机器人和2台型机器人同时工作共分拣垃圾8吨.
(1)1台型机器人和1台型机器人每小时各分拣垃圾多少吨?
(2)某垃圾处理厂计划向机器人公司购进一批型和型垃圾分拣机器人,这批机器人每小时一共能分拣垃圾20吨.设购买型机器人台,型机器人台,请用含的代数式表示;
(3)机器人公司的报价如下表:
型号 |
原价 |
购买数量少于30台 |
购买数量不少于30台 |
型 |
20万元台 |
原价购买 |
打九折 |
型 |
12万元台 |
原价购买 |
打八折 |
在(2)的条件下,设购买总费用为万元,问如何购买使得总费用最少?请说明理由.
如图,在中,以为直径的交于点,连接,且,连接并延长交的延长线于点,与相切于点.
(1)求证:是的切线;
(2)连接交于点,求证:;
(3)若,求的值.

如图1,在平面直角坐标系中,直线与直线相交于点,点是直线上的动点,过点作于点,点的坐标为,连接,.设点的纵坐标为,的面积为.
(1)当时,请直接写出点的坐标;
(2)关于的函数解析式为,其图象如图2所示,结合图1、2的信息,求出与的值;
(3)在上是否存在点,使得是直角三角形?若存在,请求出此时点的坐标和的面积;若不存在,请说明理由.
