在下列四个实数中,最小的数是
| A. |
|
B. |
|
C. |
0 |
D. |
|
某种芯片每个探针单元的面积为 ,0.00000164用科学记数法可表示为
| A. |
|
B. |
|
C. |
|
D. |
|
下列运算正确的是
| A. |
|
B. |
|
C. |
|
D. |
|
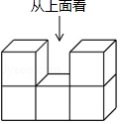
如图,一个几何体由5个相同的小正方体搭成,该几何体的俯视图是
| A. |
|
B. |
|
| C. |
|
D. |
|
不等式 的解集在数轴上表示正确的是
| A. |
|
B. |
|
| C. |
|
D. |
|
某手表厂抽查了10只手表的日走时误差,数据如下表所示(单位:
日走时误差 |
0 |
1 |
2 |
3 |
只数 |
3 |
4 |
2 |
1 |
则这10只手表的平均日走时误差(单位: 是
| A. |
0 |
B. |
0.6 |
C. |
0.8 |
D. |
1.1 |
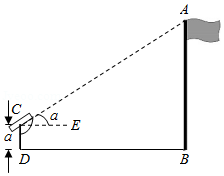
如图,小明想要测量学校操场上旗杆 的高度,他作了如下操作:(1)在点 处放置测角仪,测得旗杆顶的仰角 ;
(2)量得测角仪的高度 ;
(3)量得测角仪到旗杆的水平距离 .
利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为
| A. |
|
B. |
|
C. |
|
D. |
|
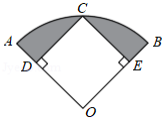
如图,在扇形 中,已知 , ,过 的中点 作 , ,垂足分别为 、 ,则图中阴影部分的面积为
| A. |
|
B. |
|
C. |
|
D. |
|
如图,在 中, ,将 绕点 按逆时针方向旋转得到△ .若点 恰好落在 边上,且 ,则 的度数为
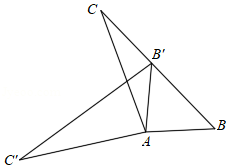
| A. |
|
B. |
|
C. |
|
D. |
|
如图,平行四边形 的顶点 在 轴的正半轴上,点 在对角线 上,反比例函数 的图象经过 、 两点.已知平行四边形 的面积是 ,则点 的坐标为
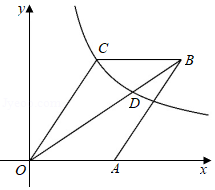
| A. |
|
B. |
, |
C. |
|
D. |
, |
使在实数范围内有意义的的取值范围是 .
若一次函数的图象与轴交于点,则 .
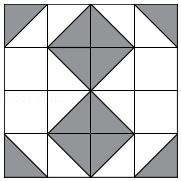
一个小球在如图所示的方格地砖上任意滚动,并随机停留在某块地砖上.每块地砖的大小、质地完全相同,那么该小球停留在黑色区域的概率是 .
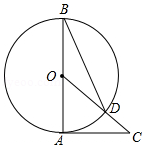
如图,已知是的直径,是的切线,连接交于点,连接.若,则的度数是 °.
若单项式与单项式是同类项,则 .
如图,在中,已知,,垂足为,.若是的中点,则 .
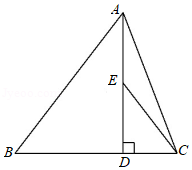
如图,在平面直角坐标系中,点、的坐标分别为、,点在第一象限内,连接、.已知,则 .

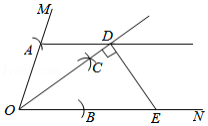
如图,已知是一个锐角,以点为圆心,任意长为半径画弧,分别交、于点、,再分别以点、为圆心,大于长为半径画弧,两弧交于点,画射线.过点作,交射线于点,过点作,交于点.设,,则 .
计算: .
解方程: .
如图,"开心"农场准备用 的护栏围成一块靠墙的矩形花园,设矩形花园的长为 ,宽为 .
(1)当 时,求 的值;
(2)受场地条件的限制, 的取值范围为 ,求 的取值范围.

为增强学生垃圾分类意识,推动垃圾分类进校园.某初中学校组织全校1200名学生参加了"垃圾分类知识竞赛",为了解学生的答题情况,学校考虑采用简单随机抽样的方法抽取部分学生的成绩进行调查分析.
(1)学校设计了以下三种抽样调查方案:
方案一:从初一、初二、初三年级中指定部分学生成绩作为样本进行调查分析;
方案二:从初一、初二年级中随机抽取部分男生成绩及在初三年级中随机抽取部分女生成绩进行调查分析;
方案三:从三个年级全体学生中随机抽取部分学生成绩进行调查分析.
其中抽取的样本具有代表性的方案是 .(填"方案一"、"方案二"或"方案三"
(2)学校根据样本数据,绘制成下表 分及以上为"优秀",60分及以上为"及格"
样本容量 |
平均分 |
及格率 |
优秀率 |
最高分 |
最低分 |
100 |
93.5 |
|
|
100 |
80 |
分数段统计(学生成绩记为 |
|||||
分数段 |
|
|
|
|
|
频数 |
0 |
5 |
25 |
30 |
40 |
请结合表中信息解答下列问题:
①估计该校1200名学生竞赛成绩的中位数落在哪个分数段内;
②估计该校1200名学生中达到"优秀"的学生总人数.
在一个不透明的布袋中装有三个小球,小球上分别标有数字0、1、2,它们除数字外都相同.小明先从布袋中任意摸出一个小球,记下数字作为平面直角坐标系内点 的横坐标,将此球放回、搅匀,再从布袋中任意摸出一个小球,记下数字作为平面直角坐标系内点 的纵坐标.请用树状图或表格列出点 所有可能的坐标,并求出点 在坐标轴上的概率.
如图,在矩形 中, 是 的中点, ,垂足为 .
(1)求证: ;
(2)若 , ,求 的长.

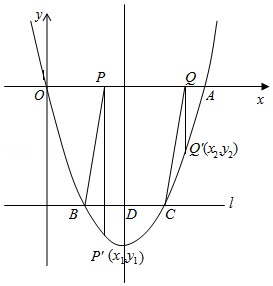
如图,二次函数 的图象与 轴正半轴交于点 ,平行于 轴的直线 与该抛物线交于 、 两点(点 位于点 左侧),与抛物线对称轴交于点 .
(1)求 的值;
(2)设 、 是 轴上的点(点 位于点 左侧),四边形 为平行四边形.过点 、 分别作 轴的垂线,与抛物线交于点 , 、 , .若 ,求 、 的值.
问题1:如图①,在四边形 中, , 是 上一点, , .求证: .
问题2:如图②,在四边形 中, , 是 上一点, , .求 的值.

某商店代理销售一种水果,六月份的销售利润 (元 与销售量 之间函数关系的图象如图中折线所示.请你根据图象及这种水果的相关销售记录提供的信息,解答下列问题:
(1)截止到6月9日,该商店销售这种水果一共获利多少元?
(2)求图象中线段 所在直线对应的函数表达式.
日期 |
销售记录 |
6月1日 |
库存 ,成本价8元 ,售价10元 (除了促销降价,其他时间售价保持不变). |
6月9日 |
从6月1日至今,一共售出 . |
6月10、11日 |
这两天以成本价促销,之后售价恢复到10元 . |
6月12日 |
补充进货 ,成本价8.5元 . |
6月30日 |
水果全部售完,一共获利1200元. |

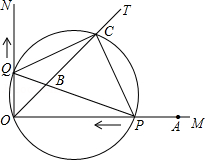
如图,已知 , 是 的平分线, 是射线 上一点, .动点 从点 出发,以 的速度沿 水平向左作匀速运动,与此同时,动点 从点 出发,也以 的速度沿 竖直向上作匀速运动.连接 ,交 于点 .经过 、 、 三点作圆,交 于点 ,连接 、 .设运动时间为 ,其中 .
(1)求 的值;
(2)是否存在实数 ,使得线段 的长度最大?若存在,求出 的值;若不存在,说明理由.
(3)求四边形 的面积.