2的绝对值是
| A. |
|
B. |
|
C. |
2 |
D. |
|
下列运算正确的是
| A. |
|
B. |
|
C. |
|
D. |
|
已知一组数据5,4,4,6,则这组数据的众数是
| A. |
4 |
B. |
5 |
C. |
6 |
D. |
8 |
如图,直线 , 被直线 所截, , ,则 的度数为

| A. |
|
B. |
|
C. |
|
D. |
|
若 ,则下列不等式一定成立的是
| A. |
|
B. |
|
C. |
|
D. |
|
将二次函数 的图象向上平移3个单位长度,得到的拋物线相应的函数表达式为
| A. |
|
B. |
|
C. |
|
D. |
|
在 中, , ,下列选项中,可以作为 长度的是
| A. |
2 |
B. |
4 |
C. |
5 |
D. |
6 |
如图,在平面直角坐标系中, 是直线 上的一个动点,将 绕点 顺时针旋转 ,得到点 ,连接 ,则 的最小值为

| A. |
|
B. |
|
C. |
|
D. |
|
分解因式: .
若代数式 有意义,则 的取值范围是 .
2020年6月30日,北斗全球导航系统最后一颗组网卫星成功定点在距离地球36000千米的地球同步轨道上,请将36000用科学记数法表示为 .
不等式组 的解集是 .
用半径为4,圆心角为 的扇形纸片围成一个圆锥的侧面,则这个圆锥的底面圆的半径为 .
已知一次函数 的图象经过 , , , 两点,则 (填" "" "或" " .
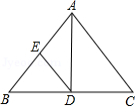
如图,在 中, , 的平分线 交 于点 , 为 的中点,若 , ,则 的长为 .
已知 , ,则 .
如图,点 在反比例函数 的图象上,点 在 轴负半轴上,直线 交 轴于点 ,若 , 的面积为6,则 的值为 .

如图,在矩形 中, , , 为 上一个动点,连接 ,线段 与线段 关于 所在的直线对称,连接 ,当点 从点 运动到点 时,线段 在平面内扫过的面积为 .

计算: .
先化简,再求值: ,其中 .
某校计划成立下列学生社团.
社团名称 |
文学社 |
动漫创作社 |
合唱团 |
生物实验小组 |
英语俱乐部 |
社团代号 |
|
|
|
|
|
为了解该校学生对上述社团的喜爱情况,学校从全体学生中随机抽取部分学生进行问卷调查(每名学生必须选一个且只能选一个学生社团).根据统计数据,绘制了如图条形统计图和扇形统计图(部分信息未给出).

(1)该校此次共抽查了 名学生;
(2)请补全条形统计图(画图后标注相应的数据);
(3)若该校共有1000名学生,请根据此次调查结果,试估计该校有多少名学生喜爱英语俱乐部?
(3)根据统计图中的数据,可以计算出该校有多少名学生喜爱英语俱乐部.
如图,在正方形 中,点 , 在 上,且 .求证:四边形 是菱形.

将4张印有"梅""兰""竹""菊"字样的卡片(卡片的形状、大小、质地都相同)放在一个不透明的盒子中,将卡片搅匀.
(1)从盒子中任意取出1张卡片,恰好取出印有"兰"字的卡片的概率为 .
(2)先从盒子中任意取出1张卡片,记录后放回并搅匀,再从中任意取出1张卡片,求取出的两张卡片中,至少有1张印有"兰"字的概率(请用画树状图或列表等方法求解).
如图,在一笔直的海岸线上有 , 两个观测站, 在 的正西方向, ,从观测站 测得船 在北偏东 的方向,从观测站 测得船 在北偏西 的方向.求船 离观测站 的距离.

如图,在 中, 是边 上一点,以 为直径的 经过点 ,且 .
(1)请判断直线 是否是 的切线,并说明理由;
(2)若 , ,求弦 的长.

某超市经销一种商品,每千克成本为50元,经试销发现,该种商品的每天销售量 (千克)与销售单价 (元 千克)满足一次函数关系,其每天销售单价,销售量的四组对应值如下表所示:
销售单价 (元 千克) |
55 |
60 |
65 |
70 |
销售量 (千克) |
70 |
60 |
50 |
40 |
(1)求 (千克)与 (元 千克)之间的函数表达式;
(2)为保证某天获得600元的销售利润,则该天的销售单价应定为多少?
(3)当销售单价定为多少时,才能使当天的销售利润最大?最大利润是多少?
【感知】如图①,在四边形 中, ,点 在边 上, ,求证: .
【探究】如图②,在四边形 中, ,点 在边 上,点 在边 的延长线上, ,且 ,连接 交 于点 .
求证: .
【拓展】如图③,点 在四边形 内, 十 ,且 ,过 作 交 于点 ,若 ,延长 交 于点 .求证: .

二次函数 的图象与 轴交于 , 两点,与 轴交于点 ,顶点为 ..
(1)求这个二次函数的表达式,并写出点 的坐标;
(2)如图①, 是该二次函数图象的对称轴上一个动点,当 的垂直平分线恰好经过点 时,求点 的坐标;
(3)如图②, 是该二次函数图象上的一个动点,连接 ,取 中点 ,连接 , , ,当 的面积为12时,求点 的坐标.
