的绝对值是
| A. |
6 |
B. |
|
C. |
|
D. |
|
如图所示的几何体是由四个完全相同的小正方体搭成的,它的俯视图是

| A. |
|
B. |
|
C. |
|
D. |
|
下列计算正确的是
| A. |
|
B. |
|
| C. |
|
D. |
|
如图, , , 的角平分线 交 于点 ,则 的度数为

| A. |
|
B. |
|
C. |
|
D. |
|
反比例函数 的图象位于
| A. |
第一象限 |
B. |
第二象限 |
C. |
第三象限 |
D. |
第四象限 |
如图,在 中, ,且 ,则 的值为
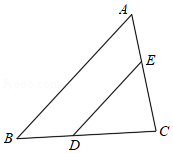
| A. |
|
B. |
|
C. |
|
D. |
|
如图, 为 的直径,点 ,点 是 上的两点,连接 , , .若 ,则 的度数是

| A. |
|
B. |
|
C. |
|
D. |
|
一元二次方程 的解为
| A. |
, |
B. |
, |
C. |
, |
D. |
, |
某射击运动员在同一条件下的射击成绩记录如下:
射击次数 |
20 |
80 |
100 |
200 |
400 |
1000 |
"射中九环以上"的次数 |
18 |
68 |
82 |
168 |
327 |
823 |
"射中九环以上"的频率(结果保留两位小数) |
0.90 |
0.85 |
0.82 |
0.84 |
0.82 |
0.82 |
根据频率的稳定性,估计这名运动员射击一次时"射中九环以上"的概率约是
| A. |
0.90 |
B. |
0.82 |
C. |
0.85 |
D. |
0.84 |
如图,在平面直角坐标系中, 的边 在 轴正半轴上,其中 , ,点 为斜边 的中点,反比例函数 的图象过点 且交线段 于点 ,连接 , ,若 ,则 的值为

| A. |
3 |
B. |
|
C. |
2 |
D. |
1 |
.
长江的流域面积大约是1800000平方千米,1800000用科学记数法表示为 .
.
从甲、乙、丙三人中选拔一人参加职业技能大赛,经过几轮初赛选拔,他们的平均成绩都是87.9分,方差分别是 , , .若选取成绩稳定的一人参加比赛,你认为适合参加比赛的选手是 .
一个圆锥的底面半径为3,高为4,则此圆锥的侧面积为 .
如图,在菱形 中,对角线 , 交于点 ,其中 , ,则菱形 的面积为 .

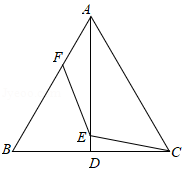
如图, 为等边三角形,边长为6, ,垂足为点 ,点 和点 分别是线段 和 上的两个动点,连接 , ,则 的最小值为 .
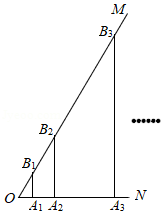
如图, ,点 在射线 上,且 ,过点 作 交射线 于点 ,在射线 上截取 ,使得 ;过点 作 交射线 于点 ,在射线 上截取 ,使得 ; ;按照此规律进行下去,则 长为 .
先化简,再求值: ,请在 的范围内选一个合适的整数代入求值.
随着"新冠肺炎"疫情防控形势日渐好转,各地开始复工复学,某校复学后成立"防疫志愿者服务队",设立四个"服务监督岗":①洗手监督岗,②戴口罩监督岗,③就餐监督岗,④操场活动监督岗.李老师和王老师报名参加了志愿者服务工作,学校将报名的志愿者随机分配到四个监督岗.
(1)李老师被分配到"洗手监督岗"的概率为 ;
(2)用列表法或画树状图法,求李老师和王老师被分配到同一个监督岗的概率.
"生活垃圾分类"逐渐成为社会生活新风尚,某学校为了了解学生对"生活垃圾分类"的看法,随机调查了200名学生(每名学生必须选择且只能选择一类看法),调查结果分为" .很有必要"" .有必要"" .无所谓"" .没有必要"四类.并根据调查结果绘制了图1和图2两幅统计图(均不完整),请根据图中提供的信息,解答下列问题:

(1)补全条形统计图;
(2)扇形统计图中" .没有必要"所在扇形的圆心角度数为 ;
(3)该校共有2500名学生,根据调查结果估计该校对"生活垃圾分类"认为" .很有必要"的学生人数.
如图,海中有一个小岛 ,它周围10海里内有暗礁,渔船跟踪鱼群由东向西航行,在 点测得小岛 在北偏西 方向上,航行12海里到达 点,这时测得小岛 在北偏西 方向上,如果渔船不改变方向继续向西航行,有没有触礁的危险?并说明理由.(参考数据:

如图, 中, , 为 的角平分线,以点 为圆心, 为半径作 与线段 交于点 .
(1)求证: 为 的切线;
(2)若 , ,求 的长.

某超市销售一款"免洗洗手液",这款"免洗洗手液"的成本价为每瓶16元,当销售单价定为20元时,每天可售出80瓶.根据市场行情,现决定降价销售.市场调查反映:销售单价每降低0.5元,则每天可多售出20瓶(销售单价不低于成本价),若设这款"免洗洗手液"的销售单价为 (元 ,每天的销售量为 (瓶 .
(1)求每天的销售量 (瓶 与销售单价 (元 之间的函数关系式;
(2)当销售单价为多少元时,销售这款"免洗洗手液"每天的销售利润最大,最大利润为多少元?
如图,在矩形 中, ,点 是线段 延长线上的一个动点,连接 ,过点 作 交射线 于点 .
(1)如图1,若 ,则 与 之间的数量关系是 ;
(2)如图2,若 ,试判断 与 之间的数量关系,写出结论并证明;(用含 的式子表示)
(3)若 ,连接 交 于点 ,连接 ,当 时,求 的长.

在平面直角坐标系中,抛物线 过点 , ,与 轴交于点 ,顶点为点 .
(1)求抛物线的解析式;
(2)点 为直线 上的一个动点,连接 ;
①如图1,是否存在点 ,使 ?若存在,求出所有满足条件的点 的坐标;若不存在,请说明理由;
②如图2,点 在 轴上方,连接 交抛物线于点 , ,点 在第三象限抛物线上,连接 ,当 时,请直接写出点 的坐标.
