计算 所得结果是
所得结果是

A. B.6C.
B.6C. D.8
D.8
下列四个实数中最小的是

A. B.2C. D.1.4
与
是同类二次根式的是

A. B. C. D.
下列命题是假命题的是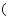
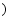
A.若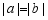 ,则
,则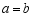
B.两直线平行,同位角相等
C.对顶角相等
D.若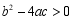 ,则方程
,则方程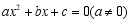 有两个不等的实数根
有两个不等的实数根
如图,正三棱柱的主视图为


A. B.
B. C.
C. D.
D.
在2016年龙岩市初中体育中考中,随意抽取某校5位同学一分钟跳绳的次数分别为:158,160,154,158,170,则由这组数据得到的结论错误的是
A.平均数为160B.中位数为158C.众数为158D.方差为20.3
反比例函数
的图象上有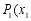 ,
,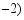 ,
, ,
, 两点,则
两点,则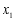 与
与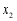 的大小关系是
的大小关系是

A.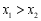 B.
B.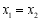 C.
C.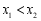 D.不确定
D.不确定
如图,在周长为12的菱形 中,
中, ,
, ,若
,若 为对角线
为对角线 上一动点,则
上一动点,则 的最小值为
的最小值为


A.1B.2C.3D.4
在一个密闭不透明的袋子里有若干个白球.为估计白球个数,小何向其中投入8个黑球,搅拌均匀后随机摸出一个球,记下颜色,再把它放入袋中,不断重复摸球400次,其中88次摸到黑球,则估计袋中大约有白球

A.18个B.28个C.36个D.42个
已知抛物线 的图象如图所示,则
的图象如图所示,则


A. B.
B. C.
C. D.
D.
分解因式: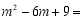 .
.
截止2016年4月28日,电影《美人鱼》的累计票房达到大约3390000000元,数据3390000000用科学记数法表示为 .
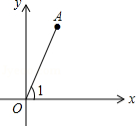
如图,若点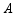 的坐标为
的坐标为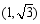 ,则
,则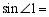 .
.
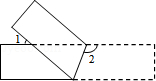
将一矩形纸条按如图所示折叠,若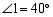 ,则
,则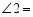
 .
.
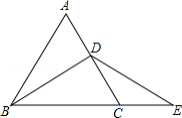
如图,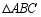 是等边三角形,
是等边三角形,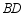 平分
平分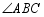 ,点
,点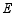 在
在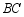 的延长线上,且
的延长线上,且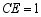 ,
,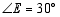 ,则
,则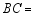 .
.
如图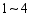 ,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依此类推,图10中有10个直角三角形的内切圆,它们的面积分别记为
,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依此类推,图10中有10个直角三角形的内切圆,它们的面积分别记为 ,
,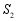 ,
,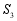 ,
, ,
,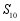 ,则
,则 .
.

计算: .
先化简再求值: ,其中 .
解不等式组: ,并把解集在数轴上表示出来.
如图, 是
是 的直径,
的直径, 是
是 上一点,
上一点, ,
, .
.
(1)求证: 是
是 的切线;
的切线;
(2)若 ,
, ,求
,求 的值.
的值.

某中学需在短跑、长跑、跳远、跳高四类体育项目中各选拔一名同学参加市中学生运动会.根据平时成绩,把各项目进入复选的学生情况绘制成如下不完整的统计图:

(1)参加复选的学生总人数为 人,扇形统计图中短跑项目所对应圆心角的度数为  ;
;
(2)补全条形统计图,并标明数据;
(3)求在跳高项目中男生被选中的概率.
图1是某公交公司1路车从起点站 站途经
站途经 站和
站和 站,最终到达终点站
站,最终到达终点站 站的格点站路线图.
站的格点站路线图. 的格点图是由边长为1的小正方形组成)
的格点图是由边长为1的小正方形组成)

(1)求1路车从 站到
站到 站所走的路程(精确到
站所走的路程(精确到 ;
;
(2)在图2、图3和图4的网格中各画出一种从 站到
站到 站的路线图.(要求:①与图1路线不同、路程相同;②途中必须经过两个格点站;③所画路线图不重复)
站的路线图.(要求:①与图1路线不同、路程相同;②途中必须经过两个格点站;③所画路线图不重复)
某网店尝试用单价随天数而变化的销售模式销售一种商品,利用30天的时间销售一种成本为10元 件的商品售后,经过统计得到此商品单价在第
件的商品售后,经过统计得到此商品单价在第 天
天 为正整数)销售的相关信息,如表所示:
为正整数)销售的相关信息,如表所示:
销售量 |
|
销售单价 |
当 |
当 |
(1)请计算第几天该商品单价为25元 件?
件?
(2)求网店销售该商品30天里所获利润 (元
(元 关于
关于 (天
(天 的函数关系式;
的函数关系式;
(3)这30天中第几天获得的利润最大?最大利润是多少?
已知 是等腰三角形,
是等腰三角形, .
.
(1)特殊情形:如图1,当 时,有
时,有
 .(填“
.(填“ ”,“
”,“  ”或“
”或“ ”
” 
(2)发现探究:若将图1中的 绕点
绕点 顺时针旋转
顺时针旋转 到图2位置,则(1)中的结论还成立吗?若成立,请给予证明;若不成立,请说明理由.
到图2位置,则(1)中的结论还成立吗?若成立,请给予证明;若不成立,请说明理由.
(3)拓展运用:如图3, 是等腰直角三角形
是等腰直角三角形 内一点,
内一点, ,且
,且 ,
, ,
, ,求
,求 的度数.
的度数.

已知抛物线
与 轴交于点
轴交于点 ,与
,与 轴的两个交点分别为
轴的两个交点分别为 ,
, .
.
(1)求抛物线的解析式;
(2)已知点 在抛物线上,连接
在抛物线上,连接 ,
, ,若
,若 是以
是以 为直角边的直角三角形,求点
为直角边的直角三角形,求点 的坐标;
的坐标;
(3)已知点 在
在 轴上,点
轴上,点 在抛物线上,是否存在以
在抛物线上,是否存在以 ,
, ,
, ,
, 为顶点的四边形是平行四边形?若存在,请直接写出点
为顶点的四边形是平行四边形?若存在,请直接写出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
