 的绝对值是
的绝对值是

A.3B. C.-
D.
.
C.-
D.
.
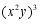 的结果是
的结果是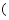
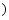
A.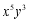 B.
B.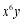 C.
C.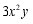 D.
D.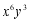
不等式组
的解集是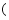
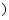
A.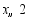 B.
B.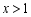 C.
C. D.无解
D.无解
如图, 和
和 相切于点
相切于点 ,
, ,则
,则 的大小为
的大小为


A. B.
B. C.
C. D.
D.
一组数据:2,5,4,3,2的中位数是

A.4B.3.2C.3D.2
如图,圆锥底面半径为 ,母线长为
,母线长为 ,其侧面展开图是圆心角为
,其侧面展开图是圆心角为 的扇形,则
的扇形,则 的值为
的值为


A.3B.6C. D.
D.
如图,已知点 ,
, ,点
,点 在直线
上,则使
在直线
上,则使 是直角三角形的点
是直角三角形的点 的个数为
的个数为


A.1B.2C.3D.4
27的立方根为 .
中国的陆地面积约为9 600  ,把9 600 000用科学记数法表示为 .
,把9 600 000用科学记数法表示为 .
因式分解: .
.
如图,在 中,
中,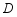 、
、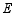 分别是边
分别是边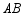 、
、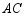 的中点,
的中点,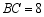 ,则
,则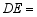 .
.

十边形的外角和是  .
.
计算: = .
如图,在 中,
中, 是斜边
是斜边 的中点,若
的中点,若 ,则
,则 .
.

如图, 的弦
的弦 、
、 相交于点
相交于点 ,若
,若 ,则
,则 .
.

找出下列各图形中数的规律,依此, 的值为 .
的值为 .

如图,在四边形 中,
中, ,
, 是
是 中点,
中点, 于点
于点 ,
, ,
, .
.
(1)若 ,则四边形
,则四边形 的面积
的面积 ;
;
(2)若 ,则此时四边形
,则此时四边形 的面积
的面积
 (用“
(用“ ”或“
”或“ ”或“
”或“ ”填空).
”填空).

计算: .
先化简,再求值: ,其中
.
,其中
.
如图, 、
、 均为等腰直角三角形,
均为等腰直角三角形, ,点
,点 在
在 上.求证:
上.求证: .
.

 、
、 两组卡片共5张,
两组卡片共5张, 中三张分别写有数字2,4,6,
中三张分别写有数字2,4,6, 中两张分别写有3,5,它们除数字外没有任何区别.
中两张分别写有3,5,它们除数字外没有任何区别.
(1)随机地从 中抽取一张,求抽到数字为2的概率;
中抽取一张,求抽到数字为2的概率;
(2)随机地分别从 、
、 中各抽取一张,请你用画树状图或列表的方法表示所有等可能的结果.现制定这样一个游戏规则:若所选出的两数之积为3的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么?
中各抽取一张,请你用画树状图或列表的方法表示所有等可能的结果.现制定这样一个游戏规则:若所选出的两数之积为3的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么?
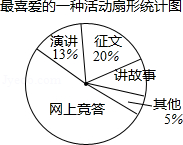
近期,我市中小学广泛开展了“传承中华文化,共筑精神家园”爱国主义读书教育活动,某中学为了解学生最喜爱的活动形式,以“我最喜爱的一种活动”为主题,进行随机抽样调查,收集数据整理后,绘制出以下两幅不完整的统计图表,请根据图中提供的信息,解答下面的问题:
最喜爱的一种活动统计表
活动形式 |
征文 |
讲故事 |
演讲 |
网上竞答 |
其他 |
人数 |
60 |
30 |
39 |
|
|
(1)在这次抽样调查中,一共调查了多少名学生?扇形统计图中“讲故事”部分的圆心角是多少度?
(2)如果这所中学共有学生3800名,那么请你估计最喜爱征文活动的学生人数.
已知反比例函数的图象经过点 .
.
(1)求该函数的解析式;
(2)若将点 沿
沿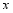 轴负方向平移3个单位,再沿
轴负方向平移3个单位,再沿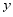 轴方向平移
轴方向平移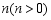 个单位得到点
个单位得到点 ,使点
,使点 恰好在该函数的图象上,求
恰好在该函数的图象上,求 的值和点
的值和点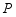 沿
沿 轴平移的方向.
轴平移的方向.
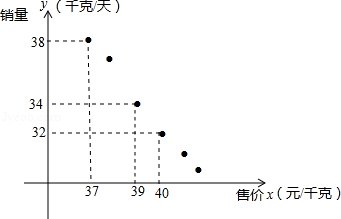
某进口专营店销售一种“特产”,其成本价是20元 千克,根据以往的销售情况描出销量
千克,根据以往的销售情况描出销量 (千克
(千克 天)与售价
天)与售价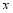 (元
(元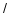 千克)的关系,如图所示.
千克)的关系,如图所示.
(1)试求出 与
与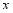 之间的一个函数关系式;
之间的一个函数关系式;
(2)利用(1)的结论:
①求每千克售价为多少元时,每天可以获得最大的销售利润.
②进口产品检验、运输等过程需耗时5天,该“特产”最长的保存期为一个月 天),若售价不低于30元
天),若售价不低于30元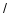 千克,则一次进货最多只能多少千克?
千克,则一次进货最多只能多少千克?
我们知道:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧;平分弧的直径垂直平分这条弧所对的弦.你可以利用这一结论解决问题:
如图,点 在以
在以 (南北方向)为直径的
(南北方向)为直径的 上,
上, ,
, 交
交 于点
于点 ,垂足为
,垂足为 ,
, ,弦
,弦 、
、 分别交
分别交 于点
于点 、
、 ,且
,且 .
.
(1)比较 与 的大小;
(2)若 ,求证:
,求证: ;
;
(3)设直线 、
、 相交所成的锐角为
相交所成的锐角为 ,试确定
,试确定 时,点
时,点 的位置.
的位置.

如图,在四边形 中,
中, ,
, ,点
,点 在边
在边 上.
上.
(1)判断四边形 的形状并加以证明;
的形状并加以证明;
(2)若 ,以过点
,以过点 的直线为轴,将四边形
的直线为轴,将四边形 折叠,使点
折叠,使点 、
、 分别落在点
分别落在点 、
、 上,且
上,且 经过点
经过点 ,折痕与四边形的另一交点为
,折痕与四边形的另一交点为 .
.
①在图2中作出四边形 (保留作图痕迹,不必说明作法和理由);
(保留作图痕迹,不必说明作法和理由);
②如果 ,那么
为何值时,
,那么
为何值时, .
.
