 等于
等于

A. B.
B. C.
C. D.
D.
方程 的根是
的根是

A. B.
B. C.
C. ,
, D.
D. ,
,
如图,点 ,
,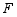 在线段
在线段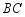 上,
上, 与
与 全等,点
全等,点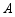 与点
与点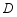 ,点
,点 与点
与点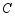 是对应顶点,
是对应顶点, 与
与 交于点
交于点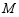 ,则
,则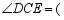


A. B.
B.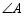 C.
C. D.
D.
不等式组
的解集是

A. B.
B. C.
C. D.
D.
如图, 是
是 的中位线,过点
的中位线,过点 作
作 交
交 的延长线于点
的延长线于点 ,则下列结论正确的是
,则下列结论正确的是


A. B.
B. C.
C. D.
D.
已知甲、乙两个函数图象上部分点的横坐标 与对应的纵坐标
与对应的纵坐标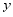 分别如表所示,两个函数图象仅有一个交点,则交点的纵坐标
分别如表所示,两个函数图象仅有一个交点,则交点的纵坐标 是
是
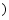
甲
|
1 |
2 |
3 |
4 |
|
0 |
1 |
2 |
3 |
乙
|
|
2 |
4 |
6 |
|
0 |
2 |
3 |
4 |
A.0B.1C.2D.3
已知 的周长是
的周长是 ,
, ,则下列直线一定为
,则下列直线一定为 的对称轴的是
的对称轴的是

A. 的边
的边 的垂直平分线
的垂直平分线
B. 的平分线所在的直线
的平分线所在的直线
C. 的边
的边 上的中线所在的直线
上的中线所在的直线
D. 的边
的边 上的高所在的直线
上的高所在的直线
已知压强的计算公式是
,我们知道,刀具在使用一段时间后,就好变钝,如果刀刃磨薄,刀具就会变得锋利.下列说法中,能正确解释刀具变得锋利这一现象的是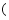

A.当受力面积一定时,压强随压力的增大而增大
B.当受力面积一定时,压强随压力的增大而减小
C.当压力一定时,压强随受力面积的减小而减小
D.当压力一定时,压强随受力面积的减小而增大
动物学家通过大量的调查估计,某种动物活到20岁的概率为0.8,活到25岁的概率为0.6,则现年20岁的这种动物活到25岁的概率是

A.0.8B.0.75C.0.6D.0.48
设 ,
, ,
,则
,
,则 ,
, ,
, 的大小关系是
的大小关系是

A. B.
B. C.
C. D.
D.
不透明的袋子里装有2个白球,1个红球,这些球除颜色外无其他差别,从袋子中随机摸出1个球,则摸出白球的概率是 .
化简: = .
如图,在 中,
中, ,且
,且 ,
, ,则
= .
,则
= .

公元3世纪,我国古代数学家刘徽就能利用近似公式
得到
的近似值.他的算法是:先将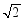 看出
看出 :由近似公式得到
;再将
看成
,由近似值公式得到
;
:由近似公式得到
;再将
看成
,由近似值公式得到
; 依此算法,所得
依此算法,所得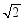 的近似值会越来越精确.当
取得近似值
时,近似公式中的
的近似值会越来越精确.当
取得近似值
时,近似公式中的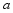 是 ,
是 ,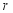 是 .
是 .
已知点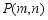 在抛物线
在抛物线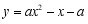 上,当
上,当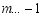 时,总有
时,总有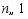 成立,则
成立,则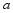 的取值范围是 .
的取值范围是 .
如图,在矩形 中,
中, ,以顶点
,以顶点 为圆心,1为半径作
为圆心,1为半径作 ,过边
,过边 上的一点
上的一点 作射线
作射线 与
与 相切于点
相切于点 ,且交边
,且交边 于点
于点 ,连接
,连接 ,若
,若 ,
, ,则
,则 的大小约为 度 分.(参考数据:
,
)
的大小约为 度 分.(参考数据:
,
)

计算: .
解方程组 .
某公司内设四个部门,2015年各部门人数及相应的每人所创年利润如表所示,求该公司2015年平均每人所创年利润.
部门 |
人数 |
每人所创年利润 |
|
1 |
36 |
|
6 |
27 |
|
8 |
16 |
|
11 |
20 |
如图, 与
与 交于点
交于点 ,
, ,
, ,
, ,求证:
,求证: .
.

已知一次函数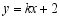 ,当
,当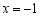 时,
时,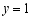 ,求此函数的解析式,并在平面直角坐标系中画出此函数图象.
,求此函数的解析式,并在平面直角坐标系中画出此函数图象.
如图,在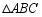 中,
中,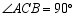 ,
,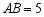 ,
,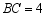 ,将
,将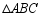 绕点
绕点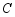 顺时针旋转
顺时针旋转 ,若点
,若点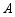 ,
,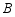 的对应点分别是点
的对应点分别是点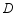 ,
, ,画出旋转后的三角形,并求点
,画出旋转后的三角形,并求点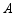 与点
与点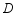 之间的距离.(不要求尺规作图)
之间的距离.(不要求尺规作图)
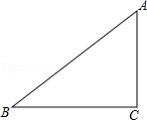
如图,在四边形 中,
中,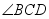 是钝角,
是钝角, ,
,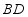 平分
平分 ,若
,若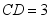 ,
,求对角线
,
,求对角线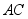 的长.
的长.

如图,是药品研究所所测得的某种新药在成人用药后,血液中的药物浓度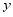 (微克
(微克 毫升)用药后的时间
毫升)用药后的时间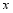 (小时)变化的图象(图象由线段
(小时)变化的图象(图象由线段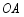 与部分双曲线
与部分双曲线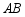 组成).并测得当
组成).并测得当 时,该药物才具有疗效.若成人用药4小时,药物开始产生疗效,且用药后9小时,药物仍具有疗效,则成人用药后,血液中药物需要多长时间达到最大浓度?
时,该药物才具有疗效.若成人用药4小时,药物开始产生疗效,且用药后9小时,药物仍具有疗效,则成人用药后,血液中药物需要多长时间达到最大浓度?

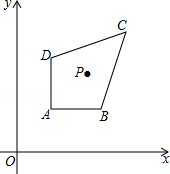
如图,在平面直角坐标系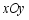 中,已知点
中,已知点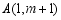 ,
,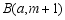 ,
,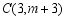 ,
,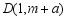 ,
,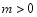 ,
,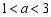 ,点
,点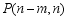 是四边形
是四边形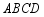 内的一点,且
内的一点,且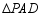 与
与 的面积相等,求
的面积相等,求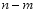 的值.
的值.
已知 是
是 的直径,点
的直径,点 在
在 上,点
上,点 在半径
在半径 上(不与点
上(不与点 ,
, 重合).
重合).
(1)如图1,若 ,
, ,求
,求 的度数.
的度数.
(2)如图2,点 在线段
在线段 上(不与
上(不与 ,
, 重合),
重合), 、
、 的延长线分别交
的延长线分别交 于点
于点 、
、 ,连接
,连接 ,
, ,点
,点 是
是 的延长线与
的延长线与 的交点,若
的交点,若 ,
, ,
, ,
, ,求
,求 的长.
的长.

已知抛物线y=-x2+bx+c与直线y=-4x+m相交于第一象限不同的两点,A(5,n),B(e,f)
(1)若点B的坐标为(3,9),求此抛物线的解析式;
(2)将此抛物线平移,设平移后的抛物线为y=-x2+px+q,过点A与点(1,2),且m-q=25,在平移过程中,若抛物线y=-x2+bx+c向下平移了S(S>0)个单位长度,求S的取值范围.