2016年黑龙江省牡丹江市中考数学试卷-优题课

下列图形中，既是轴对称图形又是中心对称图形的是（　　）

A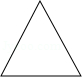．等边三角形B．正五边形

C．矩形D．平行四边形

下列计算正确的是（　　）

A． $2 a^{3} \cdot 3 a^{2} ＝ 6 a^{6}$ B． $a^{3} + 2 a^{3} ＝ 3 a^{6}$

C． $a \div b \times \frac{1}{a} ＝ a$ D． $（﹣ 2 a^{2} b ）^{3} ＝﹣ 8 a^{6} b^{3}$

由若干个小正方体搭成的几何体的主视图和俯视图，如图所示，则搭成该几何体所用的小正方体的个数最少是（　　）

A．8B．9C．10D．11

在函数 $y = \sqrt{x - 1}$ 中，自变量x的取值范围是（　　）

A． $x ＞ 1$ B． $x ＜ 1$ C． $x \leq 1$ D． $x \geq 1$

在一个口袋中有4个完全相同的小球，把它们分别标号为1，2，3，4，随机地摸出一个小球然后放回，再随机地摸出一个小球，则两次摸出的小球的标号之和等于5的概率是（　　）

A． $\frac{1}{2}$ B． $\frac{1}{3}$ C． $\frac{1}{4}$ D． $\frac{1}{5}$

在平面直角坐标系中，直线 $y ＝ 2 x ﹣ 6$ 不经过（　　）

A．第一象限B．第二象限C．第三象限D．第四象限

如图，在半径为5的⊙O中，弦 $AB ＝ 6$ ， $OP ⊥ AB$ ，垂足为点P，则OP的长为（　　）

A．3B．2.5C．4D．3.5

将抛物线 $y ＝ x^{2} ﹣ 1$ 向下平移8个单位长度后与x轴的两个交点之间的距离为（　　）

A．4B．6C．8D．10

如图，在△ABC中， $AD ⊥ BC$ ，垂足为点D，若 $AC = 6 \sqrt{2}$ ， $∠ C = 45^{\circ}$ ， $\tan ∠ ABC ＝ 3$ ，则BD等于（　　）

A．2B．3C． $3 \sqrt{2}$ D． $2 \sqrt{3}$

如图，用相同的小正方形按照某种规律进行摆放，则第8个图形中小正方形的个数是（　　）

A．71B．78C．85D．89

如图，在平面直角坐标系中， $A （﹣ 8 ，﹣ 1 ）$ ， $B （﹣ 6 ，﹣ 9 ）$ ， $C （﹣ 2 ，﹣ 9 ），$ $D （﹣ 4 ，﹣ 1 ）$ ．先将四边形ABCD沿x轴翻折，再向右平移8个单位长度，向下平移1个单位长度后，得到四边形A₁B₁C₁D₁，最后将四边形A₁B₁C₁D₁，绕着点A₁旋转，使旋转后的四边形对角线的交点落在x轴上，则旋转后的四边形对角线的交点坐标为（　　）

A．（4，0）B．（5，0）

C．（4，0）或（﹣4，0）D．（5，0）或（﹣5，0）

如图，边长为2的正方形ABCD中，AE平分∠DAC，AE交CD于点F， $CE ⊥ AE$ ，垂足为点E， $EG ⊥ CD$ ，垂足为点G，点H在边BC上， $BH ＝ DF$ ，连接AH、FH，FH与AC交于点M，以下结论：

① $FH ＝ 2 BH$ ；② $AC ⊥ FH$ ；③ $S_{△ ACF} ＝ 1$ ；④ $CE ＝ \frac{1}{2} AF$ ；⑤ $E G^{2} ＝ FG • DG$ ，

其中正确结论的个数为（　　）

A．2B．3C．4D．5

时光飞逝，小学、中学的学习时光已过去，九年的在校时间大约有16200小时，请将数16200用科学记数法表示为　　．

如图，AD和CB相交于点E， $BE ＝ DE$ ，请添加一个条件，使 $△ ABE ≌ △ CDE$ （只添一个即可），你所添加的条件是　　．

某商品的进价为每件100元，按标价打八折售出后每件可获利20元，则该商品的标价为每件　　元．

若四个互不相等的正整数中，最大的数是8，中位数是4，则这四个数的和为　　．

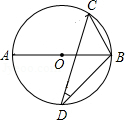
如图，AB为⊙O的直径，C，D为⊙O上的两点，若 $AB ＝ 6$ ， $BC ＝ 3$ ，则 $∠ BDC ＝$ 　　度．

已知抛物线 $y ＝ a x^{2} ﹣ 3 x + c （ a \neq 0 ）$ 经过点（﹣2，4），则 $4 a + c ﹣ 1 ＝$ 　　．

如图，在△ABC中， $AB ＝ AC ＝ 6$ ，AB的垂直平分线交AB于点E，交BC于点D，连接AD，若 $AD ＝ 4$ ，则 $DC ＝$ 　　．

在矩形ABCD中，对角线AC，BD相交于点O， $AC + BD ＝ 40$ ， $AB ＝ 12$ ，点E是BC边上一点，直线OE交CD边所在的直线于点F，若 $OE ＝ 2 \sqrt{10}$ ，则 $DF ＝$ 　　．

先化简，再求值： $\frac{x^{2} - 1}{x^{2} + x} \div (x - \frac{2 x - 1}{x})$ ，其中 $x ＝﹣ 2$ ．

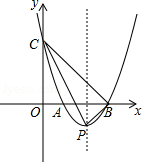
如图，在平面直角坐标系中，抛物线 $y ＝ x^{2} + bx + c$ 经过点（﹣1，8）并与x轴交于点A，B两点，且点B坐标为（3，0）．

（1）求抛物线的解析式；

（2）若抛物线与y轴交于点C，顶点为点P，求△CPB的面积．

注：抛物线 $y ＝ a x^{2} + bx + c （ a \neq 0 ）$ 的顶点坐标是 $（ - \frac{b}{2 a}, \frac{4 ac - b^{2}}{4 a} ）$

在Rt△ABC中， $∠ ACB ＝ 90 °$ ，点D为斜边AB的中点， $BC ＝ 6$ ， $CD ＝ 5$ ，过点A作 $AE ⊥ AD$ 且 $AE ＝ AD$ ，过点E作EF垂直于AC边所在的直线，垂足为点F，连接DF，请你画出图形，并直接写出线段DF的长．

为了解“足球进校园”活动开展情况，某中学利用体育课进行了定点射门测试，每人射门5次，所有班级测试结束后，随机抽取了某班学生的射门情况作为样本，对进球的人数进行整理后，绘制了不完整的统计图表，该班女生有22人，女生进球个数的众数为2，中位数为3．

女生进球个数的统计表

进球数（个）	人数
0	1
1	2
2	x
3	y
4	4
5	2

（1）求这个班级的男生人数；

（2）补全条形统计图，并计算出扇形统计图中进2个球的扇形的圆心角度数；

（3）该校共有学生1880人，请你估计全校进球数不低于3个的学生大约有　　人．

快、慢两车分别从相距180千米的甲、乙两地同时出发，沿同一路线匀速行驶，相向而行，快车到达乙地停留一段时间后，按原路原速返回甲地．慢车到达甲地比快车到达甲地早 $\frac{1}{2}$ 小时，慢车速度是快车速度的一半，快、慢两车到达甲地后停止行驶，两车距各自出发地的路程y（千米）与所用时间x（小时）的函数图象如图所示，请结合图象信息解答下列问题：

（1）请直接写出快、慢两车的速度；

（2）求快车返回过程中y（千米）与x（小时）的函数关系式；

（3）两车出发后经过多长时间相距90千米的路程？直接写出答案．

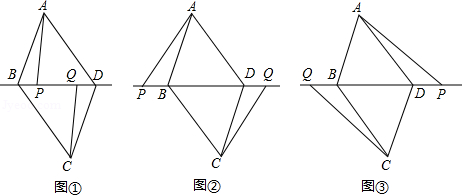
在▱ABCD中，点P和点Q是直线BD上不重合的两个动点， $AP ∥ CQ$ ，AD＝BD．

（1）如图①，求证： $BP + BQ ＝ BC$ ；

（2）请直接写出图②，图③中BP、BQ、BC三者之间的数量关系，不需要证明；

（3）在（1）和（2）的条件下，若 $DQ ＝ 1$ ， $DP ＝ 3$ ，则BC＝　　．

某绿色食品有限公司准备购进A和B两种蔬菜，B种蔬菜每吨的进价比A中蔬菜每吨的进价多0.5万元，经计算用4.5万元购进的A种蔬菜的吨数与用6万元购进的B种蔬菜的吨数相同，请解答下列问题：

（1）求A，B两种蔬菜每吨的进价；

（2）该公司计划用14万元同时购进A，B两种蔬菜，若A种蔬菜以每吨2万元的价格出售，B种蔬菜以每吨3万元的价格出售，且全部售出，请求出所获利润W（万元）与购买A种蔬菜的资金a（万元）之间的函数关系式；

（3）在（2）的条件下，要求A种蔬菜的吨数不低于B种蔬菜的吨数，若公司欲将（2）中的最大利润全部用于购买甲、乙两种型号的电脑赠给某中学，甲种电脑每台2100元，乙种电脑每台2700元，请直接写出有几种购买电脑的方案．

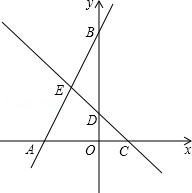
如图，在平面直角坐标系中，点O为坐标原点，直线 $y ＝﹣ x + b$ 与坐标轴交于C，D两点，直线AB与坐标轴交于A，B两点，线段OA，OC的长是方程 $x^{2} ﹣ 3 x + 2 ＝ 0$ 的两个根 $（ OA ＞ OC ）$ ．

（1）求点A，C的坐标；

（2）直线AB与直线CD交于点E，若点E是线段AB的中点，反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象的一个分支经过点E，求k的值；

（3）在（2）的条件下，点M在直线CD上，坐标平面内是否存在点N，使以点B，E，M，N为顶点的四边形是菱形？若存在，请直接写出满足条件的点N的坐标；若不存在，请说明理由．