7的相反数是
A.7B. C. D.
数据3,2,4,2,5,3,2的中位数和众数分别是
A.2,3B.4,2C.3,2D.2,2
如图是一个空心圆柱体,它的左视图是

A. B.
B.
C. D.
D.
下列二次根式中,最简二次根式是
A. B. C. D.
下列运算正确的是
A. B.
C. D.
在平面直角坐标系中,点 不可能在
A.第一象限B.第二象限C.第三象限D.第四象限
下列命题中假命题是
A.正六边形的外角和等于
B.位似图形必定相似
C.样本方差越大,数据波动越小
D.方程 无实数根
从长为3,5,7,10的四条线段中任意选取三条作为边,能构成三角形的概率是
A. B. C. D.1
如图, , , , 是 上的四个点, 是 的中点, 是半径 上任意一点.若 ,则 的度数不可能是
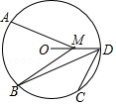
A. B. C. D.
将如图所示的抛物线向右平移1个单位长度,再向上平移3个单位长度后,得到的抛物线解析式是
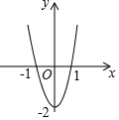
A. B. C. D.
如图,在 中, ,将 绕顶点 逆时针旋转得到△ , 是 的中点, 是 的中点,连接 .若 , ,则线段 的最大值是
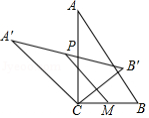
A.4B.3C.2D.1
如图,在正方形 中, 是对角线 与 的交点, 是 边上的动点(点 不与 , 重合), , 与 交于点 ,连接 , , .下列五个结论:① ;② ;③ ;④ ;⑤若 ,则 的最小值是 ,其中正确结论的个数是
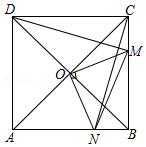
A.2B.3C.4D.5
计算: .
中国的领水面积约为 ,将数370000用科学记数法表示为 .
如图, ,点 在 上,点 在 上,如果 , ,那么 的度数为 .

如图,点 在等边 的内部,且 , , ,将线段 绕点 顺时针旋转 得到 ,连接 ,则 的值为 .

如图,在扇形 中, 是 的中点, , 与 交于点 ,以 为圆心, 的长为半径作 交 于点 ,若 , ,则图中阴影部分的面积为 .(结果保留

如图,过 作 轴, 轴,点 , 都在直线 上,若双曲线 与 总有公共点,则 的取值范围是 .

(1)计算: ;
(2)先化简,再求值: ,其中 .
尺规作图(不写作法,保留作图痕迹)
已知线段 和 ,点 在 上(如图所示).
(1)在 边上作点 ,使 ;
(2)作 的平分线;
(3)过点 作 的垂线.
如图,一次函数 的图象与反比例函数 的图象交于 , 两点,且点 的横坐标为3.
(1)求反比例函数的解析式;
(2)求点 的坐标.

在开展“经典阅读”活动中,某学校为了解全校学生利用课外时间阅读的情况,学校团委随机抽取若干名学生,调查他们一周的课外阅读时间,并根据调查结果绘制了如下尚不完整的统计表.根据图表信息,解答下列问题:
频率分布表
阅读时间 (小时) |
频数 (人 |
频率 |
|
18 |
0.12 |
|
|
|
|
45 |
0.3 |
|
36 |
|
|
21 |
0.14 |
合计 |
|
1 |
(1)填空: , , , ;
(2)将频数分布直方图补充完整(画图后请标注相应的频数);
(3)若该校由3000名学生,请根据上述调查结果,估算该校学生一周的课外阅读时间不足三小时的人数.

某次篮球联赛初赛阶段,每队有10场比赛,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分,积分超过15分才能获得参赛资格.
(1)已知甲队在初赛阶段的积分为18分,求甲队初赛阶段胜、负各多少场;
(2)如果乙队要获得参加决赛资格,那么乙队在初赛阶段至少要胜多少场?
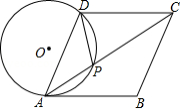
如图,在菱形 中,点 在对角线 上,且 , 是 的外接圆.
(1)求证: 是 的切线;
(2)若 , ,求 的半径.
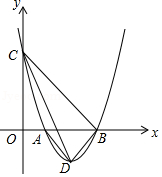
如图,抛物线 与 轴交于 , 两点,与 轴的正半轴交于点 ,其顶点为 .
(1)写出 , 两点的坐标(用含 的式子表示);
(2)设 ,求 的值;
(3)当 是直角三角形时,求对应抛物线的解析式.
已知,在 中, , , , 是 边上的一个动点,将 沿 所在直线折叠,使点 落在点 处.

(1)如图1,若点 是 中点,连接 .
①写出 , 的长;
②求证:四边形 是平行四边形.
(2)如图2,若 ,过点 作 交 的延长线于点 ,求 的长.