计算 的结果是
A . B . 1C . D . 3
某几何体的俯视图如图所示,图中数字表示该位置上的小正方体的个数,则这个几何体的主视图是

A. B.
B. C.
C. D.
D.
若一组数据为:10,11,9,8,10,9,11,9,则这组数据的众数和中位数分别是
A.9,9B.10,9C.9,9.5D.11,10
若分式 的值等于0,则 的值为
A. B.0C. D.1
下列运算正确的是
A. B. C. D.
若点 与点 关于原点成中心对称,则 的值是
A.1B.3C.5D.7
若 , 是关于 的一元二次方程 的两实根,且 ,则 等于
A. B. C.2D.3
下列命题中假命题是
A.对顶角相等B.直线 不经过第二象限
C.五边形的内角和为 D.因式分解
如图, 是 的直径, ,若 ,则圆周角 的度数是
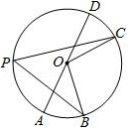
A. B. C. D.
将一条宽度为 的彩带按如图所示的方法折叠,折痕为 ,重叠部分为 (图中阴影部分),若 ,则重叠部分的面积为
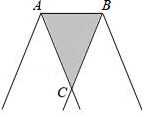
A. B. C. D.
如图,在 中,点 , 分别在 , 边上, , ,若 , ,则线段 的长为

A. B. C. D.5
如图, 是正方形 的边 的中点,点 与 关于 对称, 的延长线与 交于点 ,与 的延长线交于点 ,点 在 的延长线上,作正方形 ,连接 ,记正方形 , 的面积分别为 , ,则下列结论错误的是

A. B. C. D.
有理数9的相反数是 .
将实数 用小数表示为 .
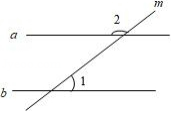
如图,直线 ,直线 与 , 均相交,若 ,则 .
若随机掷一枚均匀的骰子,骰子的6个面上分别刻有1,2,3,4,5,6点,则点数不小于3的概率是 .
如图,在扇形 中,半径 与 的夹角为 ,点 与点 的距离为 ,若扇形 恰好是一个圆锥的侧面展开图,则该圆锥的底面半径为 .

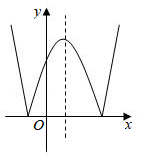
我们定义一种新函数:形如 的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数 的图象(如图所示),并写出下列五个结论:①图象与坐标轴的交点为 , 和 ;②图象具有对称性,对称轴是直线 ;③当 或 时,函数值 随 值的增大而增大;④当 或 时,函数的最小值是0;⑤当 时,函数的最大值是4.其中正确结论的个数是 .
(1)计算: ;
(2)解不等式组: ,并在数轴上表示该不等式组的解集.
尺规作图(只保留作图痕迹,不要求写出作法)
如图,已知 ,请根据“ ”基本事实作出 ,使 .

如图,菱形 的边 在 轴上,点 的坐标为 ,点 在反比例函数 的图象上,直线 经过点 ,与 轴交于点 ,连接 , .
(1)求 , 的值;
(2)求 的面积.

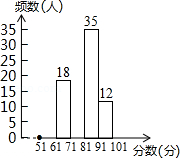
为了增强学生的安全意识,某校组织了一次全校2500名学生都参加的“安全知识”考试.阅卷后,学校团委随机抽取了100份考卷进行分析统计,发现考试成绩 分)的最低分为51分,最高分为满分100分,并绘制了如下尚不完整的统计图表.请根据图表提供的信息,解答下列问题:
分数段(分 |
频数(人 |
频率 |
|
|
0.1 |
|
18 |
0.18 |
|
|
|
|
35 |
0.35 |
|
12 |
0.12 |
合计 |
100 |
1 |
(1)填空: , , ;
(2)将频数分布直方图补充完整;
(3)该校对考试成绩为 的学生进行奖励,按成绩从高分到低分设一、二、三等奖,并且一、二、三等奖的人数比例为 ,请你估算全校获得二等奖的学生人数.
为了满足师生的阅读需求,某校图书馆的藏书从2016年底到2018年底两年内由5万册增加到7.2万册.
(1)求这两年藏书的年均增长率;
(2)经统计知:中外古典名著的册数在2016年底仅占当时藏书总量的 ,在这两年新增加的图书中,中外古典名著所占的百分率恰好等于这两年藏书的年均增长率,那么到2018年底中外古典名著的册数占藏书总量的百分之几?
如图,在矩形 中,以 边为直径作半圆 , 交 边于点 ,对角线 与半圆 的另一个交点为 ,连接 .
(1)求证: 是半圆 的切线;
(2)若 , ,求 的长.

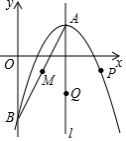
如图,已知抛物线 的顶点为 ,与 轴相交于点 ,对称轴为直线 ,点 是线段 的中点.
(1)求抛物线的表达式;
(2)写出点 的坐标并求直线 的表达式;
(3)设动点 , 分别在抛物线和对称轴 上,当以 , , , 为顶点的四边形是平行四边形时,求 , 两点的坐标.
已知: 是等腰直角三角形, ,将 绕点 顺时针方向旋转得到△ ,记旋转角为 ,当 时,作 ,垂足为 , 与 交于点 .

(1)如图1,当 时,作 的平分线 交 于点 .
①写出旋转角 的度数;
②求证: ;
(2)如图2,在(1)的条件下,设 是直线 上的一个动点,连接 , ,若 ,求线段 的最小值.(结果保留根号)