据 新闻报道,今年5月我国新能源汽车销量达到104400辆,该销量用科学记数法表示为
A. 辆B. 辆C. 辆D. 辆
如图,这是一个机械零部件,该零部件的左视图是

A. B.
B. C.
C. D.
D.
下列四个标志是关于安全警示的标志,在这些标志中,是轴对称图形的是
A. 当心吊物安全B.
当心吊物安全B. 当心触电安全
当心触电安全
C. 当心滑跌安全D.
当心滑跌安全D. 注意安全
注意安全
计算:
A. B. C. D.
反比例函数 的图象位于
A.第一、三象限B.第二、三象限C.第一、二象限D.第二、四象限
如图, , , , 是 上的点,则图中与 相等的角是

A. B. C. D.
如图,在 中,全等三角形的对数共有

A.2对B.3对C.4对D.5对
依据【资料】中所提供的信息, 年中国 的平均值大约是
A.12.30B.14.19C.19.57D.19.71
依据【资料】中所提供的信息,可以推算出中国的 要超过美国,至少要到
A.2052年B.2038年C.2037年D.2034年
已知 、 两地相距3千米,小黄从 地到 地,平均速度为4千米 小时,若用 表示行走的时间(小时), 表示余下的路程(千米),则 关于 的函数解析式是
A. B.
C. D.
小李与小陈做猜拳游戏,规定每人每次至少要出一个手指,两人出拳的手指数之和为偶数时小李获胜,那么,小李获胜的概率为

A. B. C. D.
定义:形如 的数称为复数(其中 和 为实数, 为虚数单位,规定 , 称为复数的实部, 称为复数的虚部.复数可以进行四则运算,运算的结果还是一个复数.例如 ,因此, 的实部是 ,虚部是6.已知复数 的虚部是12,则实部是
A. B.6C.5D.
计算: .
如图,若 ,则在图中所标注的角中,一定相等的角是 .

柳州市某校的生物兴趣小组在老师的指导下进行了多项有意义的生物研究并取得成果.下面是这个兴趣小组在相同的试验条件下,对某植物种子发芽率进行研究时所得到的数据:
种子数 |
30 |
75 |
130 |
210 |
480 |
856 |
1250 |
2300 |
发芽数 |
28 |
72 |
125 |
200 |
457 |
814 |
1187 |
2185 |
发芽频率 |
0.9333 |
0.9600 |
0.9615 |
0.9524 |
0.9521 |
0.9509 |
0.9496 |
0.9500 |
依据上面的数据可以估计,这种植物种子在该试验条件下发芽的概率约是 (结果精确到 .
在半径为5的圆形纸片上裁出一个边长最大的正方形纸片,则这个正方形纸片的边长应为 .
如图,在 中, , , ,则 的长为 .

已知一组数据共有5个数,它们的方差是0.4,众数、中位数和平均数都是8,最大的数是9,则最小的数是 .
计算: .
已知: .
求作: ,使得 .
作法:
①以 为圆心,任意长为半径画弧,分别交 , 于点 , ;
②画一条射线 ,以点 为圆心, 长为半径画弧,交 于点 ;
③以点 为圆心, 长为半径画弧,与第②步中所画的弧相交于点 ;
④过点 画射线 ,则 .
根据上面的作法,完成以下问题:
(1)使用直尺和圆规,作出 (请保留作图痕迹).
(2)完成下面证明 的过程(注 括号里填写推理的依据).
证明:由作法可知 , , ,
△
.

据公开报道,2017年全国教育经费总投入为42557亿元,比上年增长 ,其中投入在各学段的经费占比(即所占比例)如图,根据图中提供的信息解答下列问题.
(1)在2017年全国教育经费总投入中,义务教育段的经费总投入应该是多少亿元?
(2)2016年全国教育经费总投入约为多少亿元?(精确到

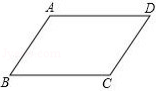
平行四边形的其中一个判定定理是:两组对边分别相等的四边形是平行四边形.请你证明这个判定定理.
已知:如图,在四边形 中, , .
求证:四边形 是平行四边形.
证明:
小张去文具店购买作业本,作业本有大、小两种规格,大本作业本的单价比小本作业本贵0.3元,已知用8元购买大本作业本的数量与用5元购买小本作业本的数量相同.
(1)求大本作业本与小本作业本每本各多少元?
(2)因作业需要,小张要再购买一些作业本,购买小本作业本的数量是大本作业本数量的2倍,总费用不超过15元.则大本作业本最多能购买多少本?
如图,直线 与 轴交于点 ,与 轴交于点 ,将线段 绕点 顺时针旋转 得到线段 ,反比例函数 的图象经过点 .
(1)求直线 和反比例函数 的解析式;
(2)已知点 是反比例函数 图象上的一个动点,求点 到直线 距离最短时的坐标.

如图, 是 的直径,弦 于点 ,点 是 上一点,且 ,连接 , , 交 于点 .
(1)若 , ,求 的半径;
(2)求证: 为等腰三角形;
(3)连接 并延长,交 的延长线于点 ,过点 作 的切线,交 的延长线于点 .求证: .

如图,直线 交 轴于点 ,交 轴于点 ,点 的坐标为 ,抛物线 经过 , , 三点,抛物线的顶点为点 ,对称轴与 轴的交点为点 ,点 关于原点的对称点为 ,连接 ,以点 为圆心, 的长为半径作圆,点 为直线 上的一个动点.
(1)求抛物线的解析式;
(2)求 周长的最小值;
(3)若动点 与点 不重合,点 为 上的任意一点,当 的最大值等于 时,过 , 两点的直线与抛物线交于 , 两点(点 在点 的左侧),求四边形 的面积.
