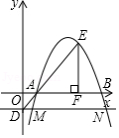
的相反数是
A. B.8C. D.
研究发现,银原子的半径约是0.00015微米,把0.00015这个数字用科学记数法表示应是
A. B. C. D.
如图,已知 是 的平分线, 于点 , 于点 , ,则 的长度是
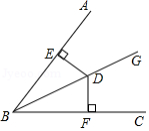
A.2B.3C.4D.6
已知 ,则它的余角是
A. B. C. D.
下列各式计算正确的是
A. B. C. D.
如图,在正方形 中, 、 、 三点的坐标分别是 、 、 ,将正方形 向右平移3个单位,则平移后点 的坐标是

A. B. C. D.
如图,在 中, , ,△ 与 关于直线 对称, ,连接 ,则 的度数是
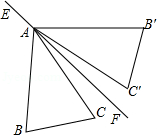
A. B. C. D.
一组数据:3,4,5, ,8的众数是5,则这组数据的方差是
A.2B.2.4C.2.8D.3
小燕一家三口在商场参加抽奖活动,每人只有一次抽奖机会:在一个不透明的箱子中装有红、黄、白三种球各1个,这些球除颜色外无其他差别,从箱子中随机摸出1个球,然后放回箱子中,轮到下一个人摸球,三人摸到球的颜色都不相同的概率是
A. B. C. D.
九年级一班同学根据兴趣分成 、 、 、 、 五个小组,把各小组人数分布绘制成如图所示的不完整统计图.则 小组的人数是

A.10人B.11人C.12人D.15人
如图, , ,则 与 的比值是
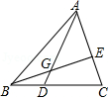
A. B. C. D.
按一定规律排列的一列数依次为:2,3,10,15,26,35, ,按此规律排列下去,则这列数中的第100个数是
A.9999B.10000C.10001D.10002
式子 在实数范围内有意义,则 的取值范围是 .
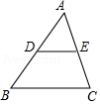
如图,已知在 中, 、 分别是 、 的中点, ,则 的长度是 .
已知直线 与反比例函数 的图象一个交点坐标为 ,则它们另一个交点的坐标是 .
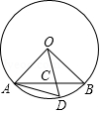
如图,已知在 中,半径 ,弦 , , 与 交于点 ,则 度.
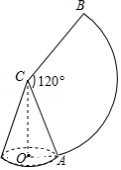
如图,圆锥侧面展开得到扇形,此扇形半径 ,圆心角 ,则此圆锥高 的长度是 .
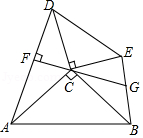
如图,点 为 与 的公共点, ,连接 、 ,过点 作 于点 ,延长 交 于点 .若 , , ,则 的值为 .
计算:
解方程: .
如图,在 中,对角线 , 相交于点 ,过点 的一条直线分别交 , 于点 , .求证: .
解不等式组 ,并求出它的整数解,再化简代数式 ,从上述整数解中选择一个合适的数,求此代数式的值.
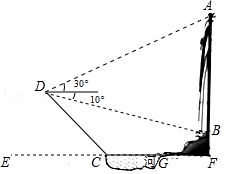
随着人们生活水平的不断提高,旅游已成为人们的一种生活时尚.为开发新的旅游项目,我市对某山区进行调查,发现一瀑布.为测量它的高度,测量人员在瀑布的对面山上 点处测得瀑布顶端 点的仰角是 ,测得瀑布底端 点的俯角是 , 与水平面垂直.又在瀑布下的水平面测得 , (注 、 、 三点在同一直线上, 于点 .斜坡 ,坡角 .求瀑布 的高度.
(参考数据: , , , , , ,
我市从2018年1月1日开始,禁止燃油助力车上路,于是电动自行车的市场需求量日渐增多.某商店计划最多投入8万元购进 、 两种型号的电动自行车共30辆,其中每辆 型电动自行车比每辆 型电动自行车多500元.用5万元购进的 型电动自行车与用6万元购进的 型电动自行车数量一样.
(1)求 、 两种型号电动自行车的进货单价;
(2)若 型电动自行车每辆售价为2800元, 型电动自行车每辆售价为3500元,设该商店计划购进 型电动自行车 辆,两种型号的电动自行车全部销售后可获利润 元.写出 与 之间的函数关系式;
(3)在(2)的条件下,该商店如何进货才能获得最大利润?此时最大利润是多少元?
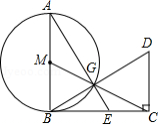
如图, 是 的直径, 是 的切线,切点为 , 是 上(除 点外)的任意一点,连接 交 于点 ,过点 作 交 的延长线于点 ,连接 并延长交 于点 .
(1)求证: ;
(2)若 ,求 的长度.
如图,抛物线 与 轴交于 、 两点, 是 轴上一点,连接 ,延长 交抛物线于点 .
(1)求此抛物线的解析式;
(2)若 点在第一象限,过点 作 轴于点 , 与 的面积比为 ,求出点 的坐标;
(3)若 是 轴上的动点,过 点作与 轴平行的直线交抛物线于 、 两点,是否存在点 ,使 ?若存在,请求出点 的坐标;若不存在,请说明理由.