的倒数是
A. B.6C. D.
下列计算正确的是
A. B.
C. D.
一个几何体的主视图和左视图都是矩形,俯视图是圆,则这个几何体是
A.圆柱B.圆锥C.球D.正方体
下列函数中,正比例函数是
A. B. C. D.
如图,钟表上10点整时,时针与分针所成的角是

A. B. C. D.
直线 向下平移2个单位,所得直线的解析式是
A. B. C. D.
正九边形的一个内角的度数是
A. B. C. D.
如图, 是 的边 的垂直平分线, 为垂足, 交 于点 ,且 , ,则 的周长是

A.12B.13C.14D.15
不等式组 的解集在数轴上表示为
A. B.
B.
C. D.
D.
某校九年级模拟考试中,1班的六名学生的数学成绩如下:96,108,102,110,108,82.下列关于这组数据的描述不正确的是
A.众数是108B.中位数是105C.平均数是101D.方差是93
如图,在半径为 的 中,弦 与 交于点 , , , ,则 的长是
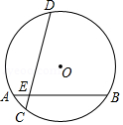
A. B. C. D.
已知 ,关于 的一元二次方程 的解为 , ,则下列结论正确的是
A. B. C. D.
计算: .
如图,已知在 中, 、 分别是 、 的中点, 、 分别是 、 的中点,且 ,则 的长度是 .

化简: .
如图, 中, , 于点 , 于点 , 与 交于点 ,则 度.
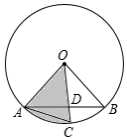
如图,已知半径为1的 上有三点 、 、 , 与 交于点 , , ,则阴影部分的扇形 面积是 .
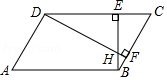
如图,在菱形 中, , ,将菱形 绕点 逆时针方向旋转,对应得到菱形 ,点 在 上, 与 交于点 ,则 的长是 .

计算: .
先化简,再求值: ,其中 .
解方程: .
一个不透明的口袋中有三个完全相同的小球,球上分别标有数字 ,1,2.第一次从袋中任意摸出一个小球(不放回),得到的数字作为点 的横坐标 ;再从袋中余下的两个小球中任意摸出一个小球,得到的数字作为点 的纵坐标 .
(1)用列表法或树状图法,列出点 的所有可能结果;
(2)求点 在双曲线 上的概率.
如图,在 中, , 为 上一点, , , .
(1)求 的长;
(2)求 的值.

我市某超市销售一种文具,进价为5元 件.售价为6元 件时,当天的销售量为100件.在销售过程中发现:售价每上涨0.5元,当天的销售量就减少5件.设当天销售单价统一为 元 件 ,且 是按0.5元的倍数上涨),当天销售利润为 元.
(1)求 与 的函数关系式(不要求写出自变量的取值范围);
(2)要使当天销售利润不低于240元,求当天销售单价所在的范围;
(3)若每件文具的利润不超过 ,要想当天获得利润最大,每件文具售价为多少元?并求出最大利润.
如图,在矩形 中, , , 平分 ,分别交 , 的延长线于点 , ;连接 ,过点 作 ,分别交 , 于点 , .
(1)求 的长;
(2)求证: .

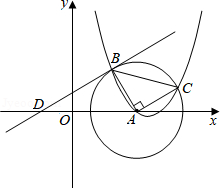
如图,已知 的圆心为点 ,抛物线 过点 ,与 交于 、 两点,连接 、 ,且 , 、 两点的纵坐标分别是2、1.
(1)请直接写出点 的坐标,并求 、 的值;
(2)直线 经过点 ,与 轴交于点 .点 (与点 不重合)在该直线上,且 ,请判断点 是否在此抛物线上,并说明理由;
(3)如果直线 与 相切,请直接写出满足此条件的直线解析式.