的绝对值是
A.2B. C. D.
如图是一个由4个相同的正方体组成的立体图形,它的主视图是

A. B.
B.
C. D.
D.
2019年6月5日,长征十一号运载火箭成功完成了“一箭七星”海上发射技术试验,该火箭重 ,将数58000用科学记数法表示为
A. B. C. D.
在平面直角坐标系中,将点 向下平移2个单位长度,得到的点 的坐标为
A. B. C. D.
不等式 的解集在数轴上表示正确的是
A. B.
B.
C. D.
D.
下列所述图形中,既是轴对称图形又是中心对称图形的是
A.等腰三角形B.等边三角形C.菱形D.平行四边形
计算 的结果是
A. B. C. D.
不透明袋子中装有红、绿小球各一个,除颜色外无其他差别,随机摸出一个小球后,放回并摇匀,再随机摸出一个,两次都摸到红球的概率为
A. B. C. D.
如图,将矩形纸片 折叠,使点 与点 重合,折痕为 ,若 , .则 的长为

A. B.4C.3D.2
如图,抛物线 与 轴相交于 、 两点,与 轴相交于点 ,点 在抛物线上,且 . 与 轴相交于点 ,过点 的直线 平行于 轴,与拋物线相交于 , 两点,则线段 的长为

A. B. C. D.
如图 , , ,则 .
某男子足球队队员的年龄分布如图所示,这些队员年龄的众数是 .

如图, 是等边三角形,延长 到点 ,使 ,连接 .若 ,则 的长为 .

我国古代数学著作《九章算术》中记载:“今有大器五小器一容三斛,大器一小器五容二斛.问大小器各容几何.”其大意为:有大小两种盛酒的桶,已知5个大桶加上1个小桶可以盛酒3斛(斛,音 ,是古代的一种容量单位).1个大桶加上5个小桶可以盛酒2斛,问1个大桶、一个小桶分别可以盛酒多少斛?若设1个大桶可以盛酒 斛,1个小桶可以盛酒 斛,根据题意,可列方程组为 .
如图,建筑物 上有一杆 .从与 相距 的 处观测旗杆顶部 的仰角为 ,观测旗杆底部 的仰角为 ,则旗杆 的高度约为 (结果取整数,参考数据: , , .

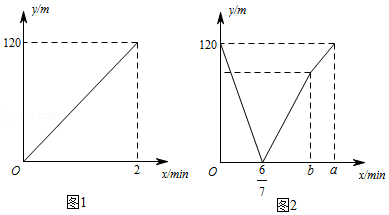
甲、乙两人沿同一条直路走步,如果两人分别从这条直路上的 , 两处同时出发,都以不变的速度相向而行,图1是甲离开 处后行走的路程 (单位: 与行走时间 (单位: 的函数图象,图2是甲、乙两人之间的距离 (单位: 与甲行走时间 (单位: 的函数图象,则 .
计算:
计算:
如图,点 , 在 上, , , ,求证: .

某校为了解八年级男生“立定跳远”成绩的情况,随机选取该年级部分男生进行测试,以下是根据测试成绩绘制的统计图表的一部分.
成绩等级 |
频数(人 |
频率 |
优秀 |
15 |
0.3 |
良好 |
||
及 格 |
||
不及格 |
5 |
根据以上信息,解答下列问题
(1)被测试男生中,成绩等级为“优秀”的男生人数为 人,成绩等级为“及格”的男生人数占被测试男生总人数的百分比为 ;
(2)被测试男生的总人数为 人,成绩等级为“不及格”的男生人数占被测试男生总人数的百分比为 ;
(3)若该校八年级共有180名男生,根据调查结果,估计该校八年级男生成绩等级为“良好”的学生人数.

某村2016年的人均收入为20000元,2018年的人均收入为24200元
(1)求2016年到2018年该村人均收入的年平均增长率;
(2)假设2019年该村人均收入的增长率与前两年的年平均增长率相同,请你预测2019年该村的人均收入是多少元?
如图,在平面直角坐标系 中,点 在反比例函数 的图象上,点 在 的延长线上, 轴,垂足为 , 与反比例函数的图象相交于点 ,连接 , .
(1)求该反比例函数的解析式;
(2)若 ,设点 的坐标为 ,求线段 的长.

如图1,四边形 内接于 , 是 的直径,过点 的切线与 的延长线相交于点 .且
(1)求证: ;
(2)过图1中的点 作 ,垂足为 (如图 ,当 , 时,求 的半径.

阅读下面材料,完成(1) (3)题
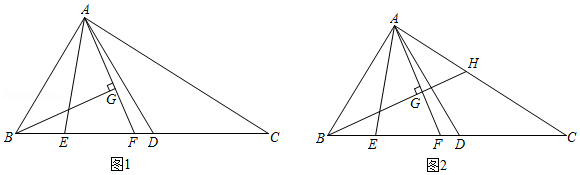
数学课上,老师出示了这样一道题:如图1, 中, ,点 、 在 上, , (其中 , 的平分线与 相交于点 , ,垂足为 ,探究线段 与 的数量关系,并证明.同学们经过思考后,交流了自己的想法:
小明:“通过观察和度量,发现 与 相等.”
小伟:“通过构造全等三角形,经过进一步推理,可以得到线段 与 的数量关系.”
老师:“保留原题条件,延长图1中的 ,与 相交于点 (如图 ,可以求出 的值.”
(1)求证: ;
(2)探究线段 与 的数量关系(用含 的代数式表示),并证明;
(3)直接写出 的值(用含 的代数式表示).
把函数 的图象绕点 旋转 ,得到新函数 的图象,我们称 是 关于点 的相关函数. 的图象的对称轴与 轴交点坐标为 .
(1)填空: 的值为 (用含 的代数式表示)
(2)若 ,当 时,函数 的最大值为 ,最小值为 ,且 ,求 的解析式;
(3)当 时, 的图象与 轴相交于 , 两点(点 在点 的右侧).与 轴相交于点 .把线段 原点 逆时针旋转 ,得到它的对应线段 ,若线 与 的图象有公共点,结合函数图象,求 的取值范围.