的相反数是
A.5B. C. D.
2019年1月1日起我国开始贯彻《国务院关于印发个人所得税专项附加扣除暂行办法的通知》的要求,此次减税范围广,其中有6500万人减税 以上,将数据6500用科学记数法表示为
A. B. C. D.
如图是由五个相同的小立方块搭成的几何体,这个几何体的俯视图是
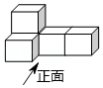
A.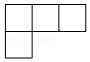 B.
B.
C.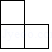 D.
D.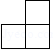
下列说法正确的是
A.若甲、乙两组数据的平均数相同, , ,则乙组数据较稳定
B.如果明天降水的概率是 ,那么明天有半天都在降雨
C.了解全国中学生的节水意识应选用普查方式
D.早上的太阳从西方升起是必然事件
下列运算正确的是
A. B.
C. D.
某青少年篮球队有12名队员,队员的年龄情况统计如下:
年龄(岁 |
12 |
13 |
14 |
15 |
16 |
人数 |
3 |
1 |
2 |
5 |
1 |
则这12名队员年龄的众数和中位数分别是
A.15岁和14岁B.15岁和15岁C.15岁和14.5岁D.14岁和15岁
已知 △ , 和 是它们的对应中线,若 , ,则 与△ 的周长比是
A. B. C. D.
已知一次函数 的图象如图所示,则 的取值范围是

A. B. C. D.
如图, 是 的直径,点 和点 是 上位于直径 两侧的点,连接 , , , ,若 的半径是13, ,则 的值是
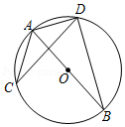
A. B. C. D.
已知二次函数 的图象如图所示,则下列结论正确的是

A. B. C. D.
因式分解: .
二元一次方程组 的解是 .
一个口袋中有红球、白球共10个,这些球除颜色外都相同.将口袋中的球搅拌均匀,从中随机摸出一个球,记下它的颜色后再放回口袋中,不断重复这一过程,共摸了100次球,发现有70次摸到红球.请你估计这个口袋中有 个白球.
如图,在四边形 中,点 , , , 分别是 , , , 的中点,若 ,则四边形 的周长是 .

如图,正比例函数 的图象与反比例函数 的图象相交于点 , ,点 是反比例函数图象上一点,它的横坐标是3,连接 , ,则 的面积是 .

如图,正方形 的对角线 上有一点 ,且 ,点 在 的延长线上,连接 ,过点 作 ,交 的延长线于点 ,连接 并延长,交 的延长线于点 ,若 , ,则线段 的长是 .

计算: .
为了丰富校园文化生活,提高学生的综合素质,促进中学生全面发展,学校开展了多种社团活动.小明喜欢的社团有:合唱社团、足球社团、书法社团、科技社团(分别用字母 , , , 依次表示这四个社团),并把这四个字母分别写在四张完全相同的不透明的卡片的正面上,然后将这四张卡片背面朝上洗匀后放在桌面上.
(1)小明从中随机抽取一张卡片是足球社团 的概率是 .
(2)小明先从中随机抽取一张卡片,记录下卡片上的字母后不放回,再从剩余的卡片中随机抽取一张卡片,记录下卡片上的字母.请你用列表法或画树状图法求出小明两次抽取的卡片中有一张是科技社团 的概率.
如图,在四边形 中,点 和点 是对角线 上的两点, , ,且 ,过点 作 交 的延长线于点 .
(1)求证:四边形 是平行四边形;
(2)若 , , ,则 的面积是 .

“勤劳”是中华民族的传统美德,学校要求同学们在家里帮助父母做一些力所能及的家务.在本学期开学初,小颖同学随机调查了部分同学寒假在家做家务的总时间,设被调查的每位同学寒假在家做家务的总时间为 小时,将做家务的总时间分为五个类别: , , , , .并将调查结果制成如下两幅不完整的统计图:

根据统计图提供的信息,解答下列问题:
(1)本次共调查了 名学生;
(2)请根据以上信息直接在答题卡中补全条形统计图;
(3)扇形统计图中 的值是 ,类别 所对应的扇形圆心角的度数是 度;
(4)若该校有800名学生,根据抽样调查的结果,请你估计该校有多少名学生寒假在家做家务的总时间不低于20小时.
2019年3月12日是第41个植树节,某单位积极开展植树活动,决定购买甲、乙两种树苗,用800元购买甲种树苗的棵数与用680元购买乙种树苗的棵数相同,乙种树苗每棵比甲种树苗每棵少6元.
(1)求甲种树苗每棵多少元?
(2)若准备用3800元购买甲、乙两种树苗共100棵,则至少要购买乙种树苗多少棵?
如图, 是 的直径, 是 的弦,直线 与 相切于点 ,过点 作 于点 .
(1)求证: ;
(2)若 , ,则 的半径是 .

在平面直角坐标系中,直线 交 轴于点 ,交 轴于点 .

(1) 的值是 ;
(2)点 是直线 上的一个动点,点 和点 分别在 轴和 轴上.
①如图,点 为线段 的中点,且四边形 是平行四边形时,求 的周长;
②当 平行于 轴, 平行于 轴时,连接 ,若 的面积为 ,请直接写出点 的坐标.
思维启迪:
(1)如图1, , 两点分别位于一个池塘的两端,小亮想用绳子测量 , 间的距离,但绳子不够长,聪明的小亮想出一个办法:先在地上取一个可以直接到达 点的点 ,连接 ,取 的中点 (点 可以直接到达 点),利用工具过点 作 交 的延长线于点 ,此时测得 米,那么 , 间的距离是 200 米.
思维探索:
(2)在 和 中, , ,且 , ,将 绕点 顺时针方向旋转,把点 在 边上时 的位置作为起始位置(此时点 和点 位于 的两侧),设旋转角为 ,连接 ,点 是线段 的中点,连接 , .
①如图2,当 在起始位置时,猜想: 与 的数量关系和位置关系分别是 ;
②如图3,当 时,点 落在 边上,请判断 与 的数量关系和位置关系,并证明你的结论;
③当 时,若 , ,请直接写出 的值.

如图,在平面直角坐标系中,抛物线 与 轴交于 , 两点(点 在点 的左侧),与 轴交于点 ,抛物线经过点 和点 ,点 是第一象限抛物线上的一个动点.

(1)求直线 和抛物线的表达式;
(2)在 轴上取点 ,连接 , ,当四边形 的面积是7时,求点 的坐标;
(3)在(2)的条件下,当点 在抛物线对称轴的右侧时,直线 上存在两点 , (点 在点 的上方),且 ,动点 从点 出发,沿 的路线运动到终点 ,当点 的运动路程最短时,请直接写出此时点 的坐标.