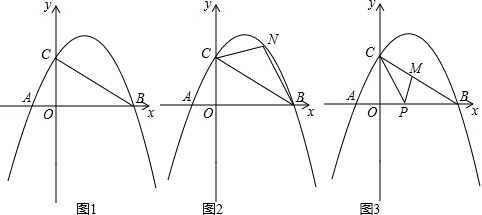
以下选项中比 小的数是
A.1B.2C. D.
如图,小明同学将一个圆锥和一个三棱柱组成组合图形,观察其三视图,其俯视图是
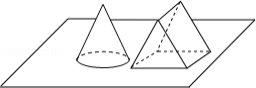
A. B.
B.
C. D.
D.
下列各式的运算正确的是
A. B. C. D.
小红把一把直尺与一块三角板如图放置,测得 ,则 的度数为
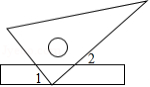
A. B. C. D.
每到四月,许多地方杨絮、柳絮如雪花般漫天飞舞,人们不堪其扰,据测定,杨絮纤维的直径约为 ,该数值用科学记数法表示为
A. B. C. D.
正比例函数 与反比例函数 部分图象如图所示,则不等式 的解集在数轴上表示正确的是
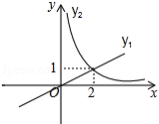
A.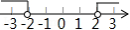 B.
B.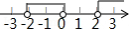
C. D.
D.
积极行动起来,共建节约型社会!我市某居民小区200户居民参加了节水行动,现统计了10户家庭一个月的节水情况,将有关数据整理如下:
节水量(单位:吨) |
0.5 |
1 |
1.5 |
2 |
家庭数(户) |
2 |
3 |
4 |
1 |
请你估计该200户家庭这个月节约用水的总量是
A.240吨B.360吨C.180吨D.200吨
2015年某县 总量为1000亿元,计划到2017年全县 总量实现1210亿元的目标.如果每年的平均增长率相同,那么该县这两年 总量的平均增长率为
A. B. C. D.
下列命题:①若 ,则 ;②平行四边形既是中心对称图形又是轴对称图形;③ 的算术平方根是3;④如果方程 有两个不相等的实数根,则实数 .其中正确的命题个数是
A.1个B.2个C.3个D.4个
如图, 为平行四边形 边 上一点, 、 分别是 、 (靠近点 的三等分点, 、 、 的面积分别为 、 、 ,若 , , ,则 的值为

A. B. C. D.4
如图是二次函数 的图象,其对称轴为 ,下列结论:① ;② ;③ ;④若 , 是抛物线上两点,则 其中结论正确的是
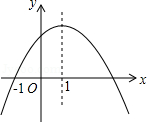
A.①②B.②③C.②④D.①③④
一个整数的所有正约数之和可以按如下方法求得,如:
,则6的所有正约数之和 ;
,则12的所有正约数之和 ;
,则36的所有正约数之和
.
参照上述方法,那么200的所有正约数之和为
A.420B.434C.450D.465
关于 的方程 一个根是1,则它的另一个根为 .
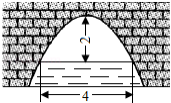
如图,一抛物线型拱桥,当拱顶到水面的距离为2米时,水面宽度为4米;那么当水位下降1米后,水面的宽度为 米.
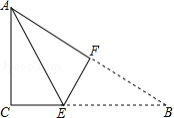
如图, 是一张直角三角形纸片, ,两直角边 、 ,现将 折叠,使点 与点 重合,折痕为 ,则 .
如图,直线 与 轴、 轴分别交于点 、 ;点 是以 为圆心、1为半径的圆上一动点,过 点的切线交线段 于点 ,则线段 的最小值是 .

(1)已知 与 是同类项,求 、 的值;
(2)先化简后求值: ,其中 .
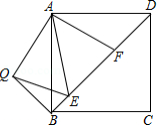
如图,在正方形 中, 、 是对角线 上两点,且 ,将 绕点 顺时针旋转 后,得到 ,连接 ,求证:
(1) 是 的平分线;
(2) .
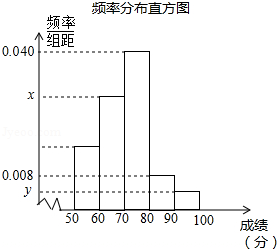
为参加学校的“我爱古诗词”知识竞赛,小王所在班级组织了一次古诗词知识测试,并将全班同学的分数(得分取正整数,满分为100分)进行统计.以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图.
组别 |
分组 |
频数 |
频率 |
1 |
|
9 |
0.18 |
2 |
|
|
|
3 |
|
20 |
0.40 |
4 |
|
0.08 |
|
5 |
|
2 |
|
合计 |
请根据以上频率分布表和频率分布直方图,回答下列问题:
(1)求出 、 、 、 的值;
(2)老师说:“小王的测试成绩是全班同学成绩的中位数”,那么小王的测试成绩在什么范围内?
(3)若要从小明、小敏等五位成绩优秀的同学中随机选取两位参加竞赛,请用“列表法”或“树状图”求出小明、小敏同时被选中的概率.(注:五位同学请用 、 、 、 、 表示,其中小明为 ,小敏为 )
随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的 型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少 ,求:
(1) 型自行车去年每辆售价多少元?
(2)该车行今年计划新进一批 型车和新款 型车共60辆,且 型车的进货数量不超过 型车数量的两倍.已知 型车和 型车的进货价格分别为1500元和1800元,计划 型车销售价格为2400元,应如何组织进货才能使这批自行车销售获利最多?
阅读理解:
我们把满足某种条件的所有点所组成的图形,叫做符合这个条件的点的轨迹.
例如:角的平分线是到角的两边距离相等的点的轨迹.
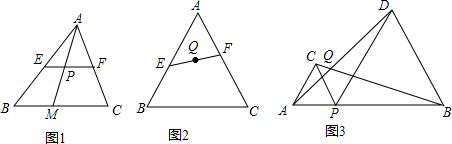
问题:如图1,已知 为 的中位线, 是边 上一动点,连接 交 于点 ,那么动点 为线段 中点.
理由: 线段 为 的中位线, ,
由平行线分线段成比例得:动点 为线段 中点.
由此你得到动点 的运动轨迹是: .
知识应用:
如图2,已知 为等边 边 、 上的动点,连接 ;若 ,且等边 的边长为8,求线段 中点 的运动轨迹的长.
拓展提高:
如图3, 为线段 上一动点(点 不与点 、 重合),在线段 的同侧分别作等边 和等边 ,连接 、 ,交点为 .
(1)求 的度数;
(2)若 ,求动点 运动轨迹的长.
如图1,抛物线 与 轴交于点 和 (点 在点 的左侧),与 轴交于点 ,连接 .
(1)求 、 的值;
(2)如图2,点 为抛物线上的一动点,且位于直线 上方,连接 、 .求 面积的最大值;
(3)如图3,点 、 分别为线段 和线段 上的动点,连接 、 ,是否存在这样的点 ,使 为等腰三角形, 为直角三角形同时成立?若存在,求出点 的坐标;若不存在,请说明理由.