计算 ,其结果为
A. B.2C.0D.
一元二次方程 根的判别式的值为
A.4B.2C.0D.
如图,直线 , 、 分别是 、 的平分线,那么下列结论错误的是

A. 与 相等B. 与 互补
C. 与 互余D. 与 不等
下列计算:(1) ,(2) ,(3) ,(4) ,其中结果正确的个数为
A.1B.2C.3D.4
若正方形的外接圆半径为2,则其内切圆半径为
A. B. C. D.1
分式方程 的解为
A. B. C.无解D.
如图,在 中, , ,点 是 延长线上的一点,且 ,则 的值为

A. B. C. D.
如图,在 中, , 为 上一点,且 , ,则 的大小为
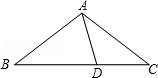
A. B. C. D.
某车间有27名工人,生产某种由一个螺栓套两个螺母的产品,每人每天生产螺母16个或螺栓22个,若分配 名工人生产螺栓,其他工人生产螺母,恰好使每天生产的螺栓和螺母配套,则下面所列方程中正确的是
A. B.
C. D.
若点 、 都在函数 为常数)的图象上,则 和 的大小关系是
A. B. C. D.不能确定
如图,点 为定角 的平分线上的一个定点,且 与 互补,若 在绕点 旋转的过程中,其两边分别与 、 相交于 、 两点,则以下结论:(1) 恒成立;(2) 的值不变;(3)四边形 的面积不变;(4) 的长不变,其中正确的个数为

A.4B.3C.2D.1
在平面直角坐标系内,直线 垂直于 轴于点 (点 在原点的右侧),并分别与直线 和双曲线 相交于点 、 ,且 ,则 的面积为
A. 或 B. 或 C. D.
计算: .
不等式组 的解集为 .
在平面直角坐标系中,点 、 的坐标分别为 、 ,现以原点为位似中心,将线段 放大得到线段 .若点 的对应点 在 轴上且 ,则点 的对应点 的坐标为 .
如图,将矩形 沿 对折,点 落在 处,点 落在 边上的 处, 与 相交于点 ,若 , , ,则 周长的大小为 .

如图,一个几何体的三视图分别是两个矩形、一个扇形,则这个几何体表面积的大小为 .

观察下列各式:
;
;
;
请利用你所得结论,化简代数式: 且 为整数),其结果为 .
(1)计算:
(2)利用所学知识以及(1)所得等式,化简代数式 .
根据要求,解答下列问题:
①方程 的解为 ;
②方程 的解为 ;
③方程 的解为 ;
(2)根据以上方程特征及其解的特征,请猜想:
①方程 的解为 ;
②关于 的方程 的解为 , .
(3)请用配方法解方程 ,以验证猜想结论的正确性.
为了考察甲、乙两种成熟期小麦的株高长势情况,现从中随机抽取6株,并测得它们的株高(单位: 如表所示:
甲 |
63 |
66 |
63 |
61 |
64 |
61 |
乙 |
63 |
65 |
60 |
63 |
64 |
63 |
(1)请分别计算表内两组数据的方差,并借此比较哪种小麦的株高长势比较整齐?
(2)现将进行两种小麦优良品种杂交实验,需从表内的甲、乙两种小麦中,各随机抽取一株进行配对,以预估整体配对状况,请你用列表法或画树状图的方法,求所抽取的两株配对小麦株高恰好都等于各自平均株高的概率.
如图,在 中,以点 为圆心, 长为半径画弧交 于点 ,再分别以点 、 为圆心,大于 的相同长为半径画弧,两弧交于点 ;连接 并延长交 于点 ,连接 ,则所得四边形 是菱形.
(1)根据以上尺规作图的过程,求证:四边形 是菱形;
(2)若菱形 的周长为16, ,求 的大小.

如图,点 是 的内心, 的延长线交 于点 ,交 的外接圆 于点 ,连接 ,过点 作直线 ,使 .
(1)求证:直线 是 的切线;
(2)求证: .

如图,直线 、 为常数)分别与 轴、 轴交于点 、 ,抛物线 与 轴交于点 .
(1)求直线 的函数解析式;
(2)若点 是抛物线 上的任意一点,设点 到直线 的距离为 ,求 关于 的函数解析式,并求 取最小值时点 的坐标;
(3)若点 在抛物线 的对称轴上移动,点 在直线 上移动,求 的最小值.
