在实数0, , ,3中,最大的是
A.0B.2C. D.3
如图所示的几何体,它的左视图是

A. B.
B.
C. D.
D.
2017年5月5日国产大型客机 首飞成功,圆了中国人的“大飞机梦”,它颜值高性能好,全长近39米,最大载客人数168人,最大航程约5550公里.数字5550用科学记数法表示为
A. B. C. D.
如图,直线 ,直线 与 , 分别相交于 , 两点, 交 于点 , ,则 的度数是

A. B. C. D.
中国古代建筑中的窗格图案美观大方,寓意吉祥,下列绘出的图案中既是轴对称图形又是中心对称图形是
A.
B.
C.
D.
化简 的结果是
A. B. C. D.
关于 的方程 的一个根为 ,则另一个根是
A. B. C.3D.6
《九章算术》是中国传统数学的重要著作,方程术是它的最高成就.其中记载:今有共买物,人出八,盈三;人出七,不足四,问人数、物价各几何?译文:今有人合伙购物,每人出8钱,会多3钱;每人出7钱,又会差4钱,问人数、物价各是多少?设合伙人数为 人,物价为 钱,以下列出的方程组正确的是
A. B.
C. D.
如图,五一旅游黄金周期间,某景区规定 和 为入口, , , 为出口,小红随机选一个入口进入景区,游玩后任选一个出口离开,则她选择从 入口进入、从 , 出口离开的概率是

A. B. C. D.
把直尺、三角尺和圆形螺母按如图所示放置于桌面上, ,若量出 ,则圆形螺母的外直径是
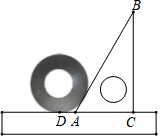
A. B. C. D.
将一次函数 的图象向上平移2个单位后,当 时, 的取值范围是
A. B. C. D.
如图,为了测量山坡护坡石坝的坡度(坡面的铅直高度与水平宽度的比称为坡度),把一根长 的竹竿 斜靠在石坝旁,量出杆长 处的 点离地面的高度 ,又量得杆底与坝脚的距离 ,则石坝的坡度为

A. B.3C. D.4
如图,正方形 的对角线 , 相交于点 , , 为 上一点, ,连接 ,过点 作 于点 ,与 交于点 ,则 的长是

A. B. C. D.
二次函数 的图象经过点 , , , ,与 轴的负半轴相交,且交点在 的上方,下列结论:① ;② ;③ ;④ .其中正确结论的个数是
A.1B.2C.3D.4
如图1,有一正方形广场 ,图形中的线段均表示直行道路, 表示一条以 为圆心,以 为半径的圆弧形道路.如图2,在该广场的 处有一路灯, 是灯泡,夜晚小齐同学沿广场道路散步时,影子长度随行走路线的变化而变化,设他步行的路程为 时,相应影子的长度为 ,根据他步行的路线得到 与 之间关系的大致图象如图3,则他行走的路线是

A. B. C. D.
分解因式: .
计算: .
在学校的歌咏比赛中,10名选手的成绩如统计图所示,则这10名选手成绩的众数是 .

如图,扇形纸叠扇完全打开后,扇形 的面积为 , , ,则 的长度为 .

如图,过点 的直线 与反比例函数 的图象交于 , 两点, ,直线 轴,与反比例函数 的图象交于点 ,连接 ,则 的面积为 .

定义:在平面直角坐标系 中,把从点 出发沿纵或横方向到达点 (至多拐一次弯)的路径长称为 , 的“实际距离”.如图,若 , ,则 , 的“实际距离”为5,即 或 .环保低碳的共享单车,正式成为市民出行喜欢的交通工具.设 , , 三个小区的坐标分别为 , , ,若点 表示单车停放点,且满足 到 , , 的“实际距离”相等,则点 的坐标为 .

(1)先化简,再求值: ,其中 .
(2)解不等式组: .
如图,在矩形 , , 于点 .求证: .

如图, 是 的直径, ,求 的度数.

某小区响应济南市提出的“建绿透绿”号召,购买了银杏树和玉兰树共150棵用来美化小区环境,购买银杏树用了12000元,购买玉兰树用了9000元.已知玉兰树的单价是银杏树单价的1.5倍,那么银杏树和玉兰树的单价各是多少?
中央电视台的“朗读者”节目激发了同学们的读书热情,为了引导学生“多读书,读好书”,某校对八年级部分学生的课外阅读量进行了随机调查,整理调查结果发现,学生课外阅读的本书最少的有5本,最多的有8本,并根据调查结果绘制了不完整的图表,如图所示:
本数(本 |
频数(人数) |
频率 |
5 |
|
0.2 |
6 |
18 |
0.36 |
7 |
14 |
|
8 |
8 |
0.16 |
合计 |
|
1 |
(1)统计表中的 , , ;
(2)请将条形统计图补充完整;
(3)求所有被调查学生课外阅读的平均本数;
(4)若该校八年级共有1200名学生,请你分析该校八年级学生课外阅读7本及以上的人数.

如图1, 的边 在 轴的正半轴上, , ,反比例函数 的图象经过的 .

(1)求点 的坐标和反比例函数的关系式;
(2)如图2,直线 分别与 轴、 轴的正半轴交于 , 两点,若点 和点 关于直线 成轴对称,求线段 的长;
(3)如图3,将线段 延长交 的图象于点 ,过 , 的直线分别交 轴、 轴于 , 两点,请探究线段 与 的数量关系,并说明理由.
某学习小组的学生在学习中遇到了下面的问题:
如图1,在
和
中,
,
,点
,
,
在同一条直线上,连接
,点
是
的中点,连接
,
,试判断
的形状并说明理由.
问题探究:
(1)小婷同学提出解题思路:先探究 的两条边是否相等,如 ,以下是她的证明过程
证明:延长线段 交 的延长线于点 . 是 的中点, . , . |
. 又 , . . . |
请根据以上证明过程,解答下列两个问题:
①在图1中作出证明中所描述的辅助线;
②在证明的括号中填写理由(请在 , , , 中选择).
(2)在(1)的探究结论的基础上,请你帮助小婷求出 的度数,并判断 的形状.
问题拓展:
(3)如图2,当 绕点 逆时针旋转某个角度时,连接 ,延长 交 的延长线于点 ,其他条件不变,判断 的形状并给出证明.
如图1,矩形 的顶点 , 的坐标分别为 , ,直线 交 于点 , ,抛物线 过 , 两点.

(1)求点 的坐标和抛物线 的表达式;
(2)点 是抛物线 对称轴上一动点,当 时,求所有符合条件的点 的坐标;
(3)如图2,点 ,连接 ,将抛物线 的图象向下平移 个单位得到抛物线 .
①设点 平移后的对应点为点 ,当点 恰好在直线 上时,求 的值;
②当 时,若抛物线 与直线 有两个交点,求 的取值范围.