在 、1、 、2这四个数中,最小的数是
A. B.1C. D.2
如图,下列各组角中,互为对顶角的是

A. 和 B. 和 C. 和 D. 和
4的平方根是
A.2B. C. D.16
下列图形中,属于中心对称图形的是
A. B.
B. C.
C. D.
D.
若一组数据:1、2、 、4、5的众数为5,则这组数据的中位数是
A.1B.2C.4D.5
下列运算正确的是
A. B. C. D.
下列各式分解因式正确的是
A. B.
C. D.
如图,这是一个几何体的三视图,根据图中所示数据计算这个几何体的侧面积为

A. B. C. D.
如图, 在同一平面直角坐标系中, 一次函数 、 是常数, 且 与反比例函数 是常数, 且 的图象相交于 , 两点, 则不等式 的解集是

A . B . 或 C . 或 D .
如图,在 中, , ,垂足为 , 是边 的中点, ,则 的长为

A. B. C.6D.
如图, 是 的直径,且经过弦 的中点 ,已知 , ,则 的长为
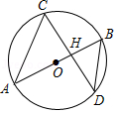
A. B. C. D.
如图,正方形 的边长为1,以对角线 为边作第二个正方形 ,再以对角线 为边作第三个正方形 ,依此下去,第 个正方形的面积为

A. B. C. D.
要使二次根式 有意义,则 的取值范围是 .
医学家发现了一种病毒,其长度约为 ,用科学记数法表示为 .
从 、0、 、 、5.1、7这6个数中随机抽取一个数,抽到无理数的概率是 .
如图,将 绕直角顶点 顺时针旋转 ,得到△ ,连接 ,若 ,则 的度数是 .

某种商品每件进价为20元,调查表明:在某段时间内若以每件 元 ,且 为整数)出售,可卖出 件,若使利润最大,则每件商品的售价应为 元.
如图,正方形 的边长为12,点 在边 上, ,过点 作 ,分别交 、 于 、 两点.若点 、 分别为 、 的中点,则 的长为 .

计算: .
解分式方程: .
某中学为了了解学生每周在校体育锻炼时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表,请根据图表信息解答下列问题:
时间(小时) |
频数(人数) |
频率 |
|
4 |
0.1 |
|
10 |
0.25 |
|
|
0.15 |
|
8 |
|
|
12 |
0.3 |
合计 |
40 |
1 |
(1)表中的 , ;
(2)请将频数分布直方图补全;
(3)若该校共有1200名学生,试估计全校每周在校参加体育锻炼时间至少有4小时的学生约为多少名?

如图,一艘游轮在 处测得北偏东 的方向上有一灯塔 .游轮以 海里 时的速度向正东方向航行2小时到达 处,此时测得灯塔 在 处北偏东 的方向上,求 处与灯塔 相距多少海里?(结果精确到1海里,参考数据: ,

某自行车经销商计划投入7.1万元购进100辆 型和30辆 型自行车,其中 型车单价是 型车单价的6倍少60元.
(1)求 、 两种型号的自行车单价分别是多少元?
(2)后来由于该经销商资金紧张,投入购车的资金不超过5.86万元,但购进这批自行车的总数不变,那么至多能购进 型车多少辆?
如图,在 中, , 、 分别是边 、 的中点,过点 作 交 的延长线于点 ,连接 .
(1)求证:四边形 是菱形;
(2)若四边形 的面积为24, ,求 的长.

如图, 是 的弦,过 的中点 作 ,垂足为 ,过点 作直线 交 的延长线于点 ,使得 .
(1)求证: 是 的切线;
(2)若 , ,求 的面积.

如图,在平面直角坐标系中,抛物线 交 轴于 、 两点 在 的左侧),且 , ,与 轴交于 ,抛物线的顶点坐标为 .
(1)求 、 两点的坐标;
(2)求抛物线的解析式;
(3)过点 作直线 轴,交 轴于点 ,点 是抛物线上 、 两点间的一个动点(点 不与 、 两点重合), 、 与直线 分别交于点 、 ,当点 运动时, 是否为定值?若是,试求出该定值;若不是,请说明理由.
