6的相反数是
A. B. C.6D.
如图,已知 , ,则 的大小为

A. B. C. D.
下列计算正确的是
A. B.
C. D.
截至2010年“费尔兹奖”得主中最年轻的8位数学家获奖时的年龄分别为29,28,29,31,31,31,29,31,则由年龄组成的这组数据的中位数是
A.28B.29C.30D.31
已知关于 的方程 有两个相等的实数根,则常数 的值为
A. B.0C.1D.3
如图,在 中, 是 边上的高, 平分 交 边于 , , ,则 的大小是
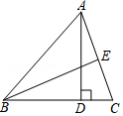
A. B. C. D.
下列说法中,正确的有
①一组数据的方差越大,这组数据的波动反而越小;②一组数据的中位数只有一个;
③在一组数据中,出现次数最多的数据称为这组数据的众数.
A.①②B.①③C.②③D.①②③
一个圆柱的侧面展开图是边长为 的正方形,则这个圆柱的体积为
A. B. C. D.
下列命题中,是假命题的是
A.任意多边形的外角和为
B.在 和△ 中,若 , , ,则 △
C.在一个三角形中,任意两边之差小于第三边
D.同弧所对的圆周角和圆心角相等
如图,点 、 分别是 的内接正三角形 的 、 边上的中点,若 的半径为2,则 的长等于
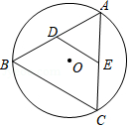
A. B. C.1D.
如图,将 沿 翻折得到 ,再将 绕 点逆时针旋转 得到 ,延长 交 于 .已知 , , ,则四边形 的面积为
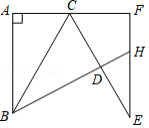
A. B. C. D.
当 时,函数 的图象上至少有一点在函数 的图象下方,则 的取值范围为
A. B. C. D.
计算: .
某校欲招聘一名数学老师,甲、乙两位应试者经审查符合基本条件,参加了笔试和面试,他们的成绩如右表所示,请你按笔试成绩占 ,面试成绩占 选出综合成绩较高的应试者是 .
应试者 |
笔试成绩 |
面试成绩 |
甲 |
80 |
90 |
乙 |
85 |
86 |
如图所示,某拦水大坝的横断面为梯形 , 、 为梯形的高,其中迎水坡 的坡角 ,坡长 米,背水坡 的坡度 为 与 的比值),则背水坡 的坡长为 米.

若抛物线 与 轴交于 、 两点 为常数, , 为自然数, ,用 表示 、 两点间的距离,则 .
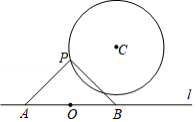
如图,已知 的半径为3,圆外一定点 满足 ,点 为 上一动点,经过点 的直线 上有两点 、 ,且 , , 不经过点 ,则 的最小值为 .
计算: .
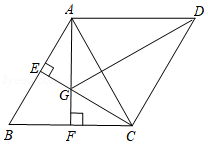
如图,在平行四边形 中, 、 分别是 、 的中点, ,垂足为 , ,垂足为 , 与 相交于点 .
(1)证明: .
(2)若 ,求四边形 的对角线 的长.
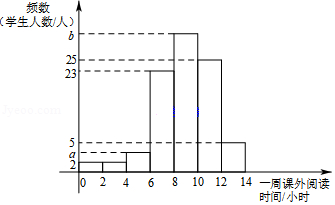
为了解学生的课外阅读情况,某市教育局在某校学生中随机抽取了100名学生进行调研,获得了他们一周的课外阅读时间的相关数据,通过整理得到如下的频数分布直方图.
(1)已知阅读时间在 之间的学生的频率为0.4,求 、 的值.
(2)在样本数据中,从阅读时间在 之间与在 之间的两个时间段内的学生中随机选取2名学生,请用列举法求出任选的2人中恰有1人一周阅读时间在 之间的概率.
(3)该校规定一周课外阅读时间在10小时及以上的学生,可申请“博闻阅读”项目的资助,如果该校共有学生3000名,用样本估计该校可申请“博闻阅读”项目资助的学生人数.
为了吸引游客,某景区通过加强对服务人员的培训、增建索道和开发新景点等措施,对景区品质进行提档升级,升级后游客人数平均每月是升级前的1.1倍还多3000人,且在 个月时间内,升级前只能达36万游客,而升级后可达43.2万游客.
(1)问升级前和升级后平均每月各有多少万游客?
(2)现在景区内去极险峰的索道票价为80元 张,为了确保景区索道运营有利润,又要保障游客安全,需使每天卖出的索道票总金额超过2万元而票数不超过1000张,问景区每天卖出的索道票数的范围.
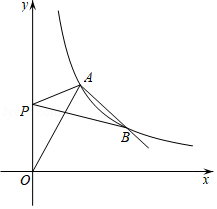
如图,函数 的图象与双曲线 相交于点 和点 .
(1)求双曲线的解析式及点 的坐标;
(2)若点 在 轴上,连接 , ,求当 的值最小时点 的坐标.
如图,已知 、 为 的两条直径, 为切线,过 上一点 作 于 ,连接 并延长交 于点 ,连接 .
(1)求证: .
(2)设 为点 关于 对称点,连接 、 ,如果 , 的半径为3,求 的值.

如图,在平面直角坐标系 中,抛物线 与 轴交于 、 两点,与 轴的负半轴交于点 ,其中 , .
(1)求抛物线 及直线 的解析式.
(2)沿直线 由 至 的方向平移抛物线 ,得到新的抛物线 , 上的点 为 上的点 的对应点,若抛物线 恰好经过点 ,同时与 轴交于另一点 ,连接 、 ,试判断 的形状,并说明理由.
(3)在(2)的条件下,若 为线段 (不含端点)上一动点,作 于 , 于点 ,设 , .试判断 的值是否存在最大值?若存在,求出这个最大值,并求出此时点 的坐标;如不存在,请说明理由.
