A.1B. C.2020D.
如图,下列几何体的左视图不是矩形的是
A. B.
B. C.
C. D.
D.
点 关于 轴对称的点 的坐标是
A. B. C. D.
已知一组数据1,0,3, , ,2,3的平均数是1,则这组数据的众数是
A. B.3C. 和3D.1和3
一元二次方程 的根为
A. B. C. 或 D. 或
下列等式成立的是
A. B.
C. D.
若一次函数 的图象不经过第二象限,则 的取值范围是
A. B. C. D.
点 是线段 的中点,点 是线段 的三等分点.若线段 ,则线段 的长为
A. B. C. 或 D. 或
下列命题是真命题的是
A.顶点在圆上的角叫圆周角
B.三点确定一个圆
C.圆的切线垂直于半径
D.三角形的内心到三角形三边的距离相等
如图所示, 的顶点在正方形网格的格点上,则 的值为
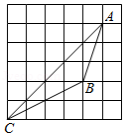
A. B. C.2D.
如图,等边三角形 和正方形 都内接于 ,则

A. B. C. D.
二次函数 的图象如图所示,有如下结论:
① ;
② ;
③ ;
④ 为实数).
其中正确结论的个数是
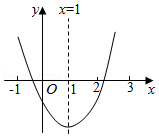
A.1个B.2个C.3个D.4个
函数 中,自变量 的取值范围是 .
因式分解: .
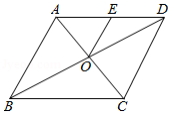
如图, 的对角线 、 相交于点 , 交 于点 ,若 , 的周长等于5,则 的周长等于 .
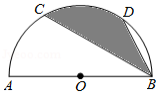
如图,点 、 分别是半圆 上的三等分点,若阴影部分的面积是 ,则半圆的半径 的长为 .
如图,矩形 的面积为 ,对角线 与双曲线 相交于点 ,且 ,则 的值为 .

解方程: .
化简求值: ,其中 .
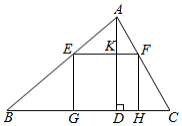
如图,一块材料的形状是锐角三角形 ,边 ,高 ,把它加工成正方形零件,使正方形的一边在 上,其余两个顶点分别在 、 上,这个正方形零件的边长是多少?
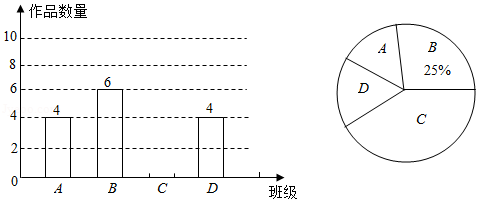
某校团委在“五 四”青年节举办了一次“我的中国梦”作文大赛,分三批对全校20个班的作品进行评比.在第一批评比中,随机抽取 、 、 、 四个班的征集作品,对其数量进行统计后,绘制如图两幅不完整的统计图.
(1)第一批所抽取的4个班共征集到作品 件;在扇形统计图中表示 班的扇形的圆心角的度数为 ;
(2)补全条形统计图;
(3)第一批评比中, 班 班各有一件、 班 班各有两件作品获得一等奖.现要在获得一等奖的作品中随机抽取两件在全校展出,用树状图或列表法求抽取的作品来自两个不同班级的概率.
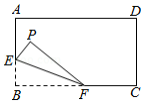
如图, 是半圆 的直径, 是半圆上的一点, 平分 交半圆于点 ,过点 作 与 的延长线交于点 .
(1)求证: 是半圆的切线;
(2)若 , ,求半圆的直径.

若不等式组 恰有四个整数解,则 的取值范围是 .
如图,矩形 中, , , 是 上一点,且 , 是 上一动点,若将 沿 对折后,点 落在点 处,则点 到点 的最短距离为 .
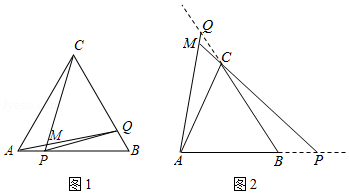
如图,点 、 分别是等边 边 、 上的动点(端点除外),点 、点 以相同的速度,同时从点 、点 出发.
(1)如图1,连接 、 .求证: ;
(2)如图1,当点 、 分别在 、 边上运动时, 、 相交于点 , 的大小是否变化?若变化,请说明理由;若不变,求出它的度数;
(3)如图2,当点 、 在 、 的延长线上运动时,直线 、 相交于 , 的大小是否变化?若变化,请说明理由;若不变,求出它的度数.
如图,已知直线 .
(1)当反比例函数 的图象与直线 在第一象限内至少有一个交点时,求 的取值范围.
(2)若反比例函数 的图象与直线 在第一象限内相交于点 , 、 , ,当 时,求 的值,并根据图象写出此时关于 的不等式 的解集.

如图, 的半径为 ,其内接锐角三角形 中, 、 、 所对的边分别是 、 、 .
(1)求证: ;
(2)若 , , ,利用(1)的结论求 的长和 的值.

如图,二次函数 的图象过 、 、 , 三点.
(1)求二次函数的解析式;
(2)若线段 的垂直平分线与 轴交于点 ,与二次函数的图象在 轴上方的部分相交于点 ,求直线 的解析式;
(3)在直线 下方的二次函数的图象上有一动点 ,过点 作 轴,交直线 于 ,当线段 的长最大时,求点 的坐标.
