下列各数是有理数的是
A. B. C. D.
地球绕太阳公转的速度约为 ,则110000用科学记数法可表示为
A. B. C. D.
下列图形中既是轴对称图形,又是中心对称图形的是
A. B.
B.
C. D.
D.
下列运算正确的是
A. B. C. D.
如图,该几何体主视图是

A. B.
B. C.
C. D.
D.
下表是某位男子马拉松长跑运动员近6次的比赛成绩(单位:分钟)
第几次 |
1 |
2 |
3 |
4 |
5 |
6 |
比赛成绩 |
145 |
147 |
140 |
129 |
136 |
125 |
则这组成绩的中位数和平均数分别为
A.137、138B.138、137C.138、138D.137、139
如图, 中, 为 边的中点, , , , ,则

A. B. C. D.
如图,是二次函数 的图象,对下列结论:① ,② ,③ ,其中错误的个数是

A.3B.2C.1D.0
如图,已知 为四边形 的外接圆, 为圆心,若 , ,则 的半径长为

A. B. C. D.
如图,已知凸五边形 的边长均相等,且 , ,则 必定满足

A. B.
C. D.以上情况均有可能
因式分解: .
分式方程 的解为 .
如图,已知扇形 的圆心角为 ,扇形的面积为 ,则该扇形的弧长为 .

如图所示,为了测量出一垂直水平地面的某高大建筑物 的高度,一测量人员在该建筑物附近 处,测得建筑物顶端 处的仰角大小为 ,随后沿直线 向前走了100米后到达 处,在 处测得 处的仰角大小为 ,则建筑物 的高度约为 米.
(注:不计测量人员的身高,结果按四舍五入保留整数,参考数据: ,

甲、乙两位同学各抛掷一枚质地均匀的骰子,他们抛掷的点数分别记为 、 ,则 的概率为 .
观察下列等式:
请按上述规律,写出第 个式子的计算结果 为正整数) .(写出最简计算结果即可)
计算: .
先化简,再求值: ,其中 .
已知关于 的不等式组 恰好有两个整数解,求实数 的取值范围.
已知关于 的一元二次方程
(1)求证:该方程有两个不等的实根;
(2)若该方程的两实根 、 满足 ,求 的值.
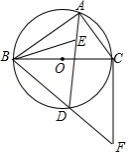
如图, 是 的外接圆, 为 的直径,点 为 的内心,连接 并延长交 于 点,连接 并延长至 ,使得 ,连接 、 .
(1)求证: ;
(2)求证:直线 为 的切线.
随着社会的发展,私家车变得越来越普及,使用节能低油耗汽车,对环保有着非常积极的意义,某市有关部门对本市的某一型号的若干辆汽车,进行了一项油耗抽样实验:即在同一条件下,被抽样的该型号汽车,在油耗 的情况下,所行驶的路程(单位: 进行统计分析,结果如图所示:

(注:记 为 , 为 , 为 , 为 , 为
请依据统计结果回答以下问题:
(1)试求进行该试验的车辆数;
(2)请补全频数分布直方图;
(3)若该市有这种型号的汽车约900辆(不考虑其他因素),请利用上述统计数据初步预测,该市约有多少辆该型号的汽车,在耗油 的情况下可以行驶 以上?
小明同学在一次社会实践活动中,通过对某种蔬菜在1月份至7月份的市场行情进行统计分析后得出如下规律:
①该蔬菜的销售单价 (单位:元 千克)与时间 (单位:月份)满足关系: ;
②该蔬菜的平均成本 (单位:元 千克)与时间 (单位:月份)满足二次函数关系 .
已知4月份的平均成本为2元 千克,6月份的平均成本为1元 千克.
(1)求该二次函数的解析式;
(2)请运用小明统计的结论,求出该蔬菜在第几月份的平均利润 (单位:元 千克)最大?最大平均利润是多少?(注:平均利润 销售单价 平均成本)
在现实生活中,我们经常会看到许多“标准”的矩形,如我们的课本封面、 的打印纸等,其实这些矩形的长与宽之比都为 ,我们不妨就把这样的矩形称为“标准矩形”,在“标准矩形” 中, 为 边上一定点,且 ,如图所示.
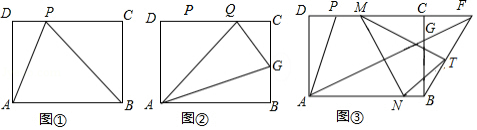
(1)如图①,求证: ;
(2)如图②,点 在 上,且 ,若 为 边上一动点,当 的周长最小时,求 的值;
(3)如图③,已知 ,在(2)的条件下,连接 并延长交 的延长线于点 ,连接 , 为 的中点, 、 分别为线段 与 上的动点,且始终保持 ,请证明: 的面积 为定值,并求出这个定值.
如图,直线 与函数 的图象相交于 、 两点,与 轴相交于 点,过 、 两点作 轴的垂线,垂足分别为 、 ,过 、 两点作 轴的垂线,垂足分别为 、 ;直线 与 相交于点 ,连接 .设 、 两点的坐标分别为 、 ,其中 .
(1)如图①,求证: ;
(2)如图②,若 、 、 、 四点在同一圆周上,求 的值;
(3)如图③,已知 ,且点 在直线 上,试问:在线段 上是否存在点 ,使得 ?如存在,请求出点 的坐标;若不存在,请说明理由.
