的倒数是
A. B. C.2D.
随着经济发展,人民的生活水平不断提高,旅游业快速增长,2016年国民出境旅游超过120 000 000人次,将120 000 000用科学记数法表示为
A. B. C. D.
下列图形中既是轴对称图形,又是中心对称图形的是
A. B.
B.
C. D.
D.
含 角的直角三角板与直线 、 的位置关系如图所示,已知 , ,则

A. B. C. D.
下列说法正确的是
A.打开电视,它正在播广告是必然事件
B.要考察一个班级中的学生对建立生物角的看法适合用抽样调查
C.在抽样调查过程中,样本容量越大,对总体的估计就越准确
D.甲、乙两人射中环数的方差分别为 , ,说明乙的射击成绩比甲稳定
若 ,则
A.0B. C.0或 D.1或 2
如图是“明清影视城”的一扇圆弧形门,小红到影视城游玩,他了解到这扇门的相关数据:这扇圆弧形门所在的圆与水平地面是相切的, 米, 米,且 、 与水平地面都是垂直的.根据以上数据,请你帮小红计算出这扇圆弧形门的最高点离地面的距离是

A.2米B.2.5米C.2.4米D.2.1米
已知 ,则下列三个等式:① ,② ,③ 中,正确的个数有
A.0个B.1个C.2个D.3个
已知二次函数 为常数),当 时,函数值 的最小值为 ,则 的值是
A. B. C. 或 D. 或
如图,平面直角坐标系 中,矩形 的边 、 分别落在 、 轴上,点 坐标为 ,反比例函数 的图象与 边交于点 ,与 边交于点 ,连接 ,将 沿 翻折至△ 处,点 恰好落在正比例函数 图象上,则 的值是

A. B. C. D.
.
二元一次方程组 的解是 .
如图,直线 、 垂直相交于点 ,曲线 关于点 成中心对称,点 的对称点是点 , 于点 , 于点 .若 , ,则阴影部分的面积之和为 .

点 、 、 在格点图中的位置如图所示,格点小正方形的边长为1,则点 到线段 所在直线的距离是 .

庄子说:“一尺之椎,日取其半,万世不竭”.这句话(文字语言)表达了古人将事物无限分割的思想,用图形语言表示为图1,按此图分割的方法,可得到一个等式(符号语言) .

图2也是一种无限分割:在 中, , ,过点 作 于点 ,再过点 作 于点 ,又过点 作 于点 ,如此无限继续下去,则可将利 分割成 、△ 、△ 、△ 、 、△ 、 .假设 ,这些三角形的面积和可以得到一个等式是 .
对于函数 ,我们定义 、 为常数).
例如 ,则 .
已知: .
(1)若方程 有两个相等实数根,则 的值为 ;
(2)若方程 有两个正数根,则 的取值范围为 .
计算: .
求不等式组 的所有整数解.
如图,延长 的边 到 ,使 ,延长 到点 ,使 ,分别连接点 、 和 、 .求证: .
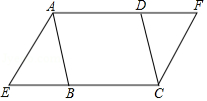
化简: .
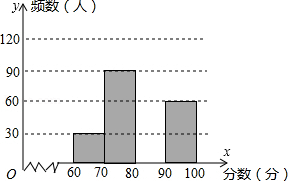
为了了解我市中学生参加“科普知识”竞赛成绩的情况,随机抽查了部分参赛学生的成绩,整理并制作出如下的统计表和统计图,如图所示.请根据图表信息解答下列问题:
组别 |
分数段(分 |
频数 |
频率 |
组 |
|
30 |
0.1 |
组 |
|
90 |
|
组 |
|
|
0.4 |
组 |
|
60 |
0.2 |
(1)在表中: , ;
(2)补全频数分布直方图;
(3)小明的成绩是所有被抽查学生成绩的中位数,据此推断他的成绩在 组;
(4)4个小组每组推荐1人,然后从4人中随机抽取2人参加颁奖典礼,恰好抽中 、 两组学生的概率是多少?并列表或画树状图说明.
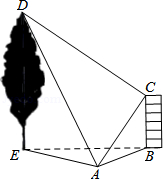
如图,在水平地面上有一幢房屋 与一棵树 ,在地面观测点 处测得屋顶 与树梢 的仰角分别是 与 , ,在屋顶 处测得 .若房屋的高 米,求树高 的长度.
某公司从2013年开始投入技术改进资金,经技术改进后,其产品的成本不断降低,具体数据如下表:
年 度 |
2013 |
2014 |
2015 |
2016 |
投入技改资金 (万元) |
2.5 |
3 |
4 |
4.5 |
产品成本 (万元 件) |
7.2 |
6 |
4.5 |
4 |
(1)请你认真分析表中数据,从一次函数和反比例函数中确定哪一个函数能表示其变化规律,给出理由,并求出其解析式;
(2)按照这种变化规律,若2017年已投入资金5万元.
①预计生产成本每件比2016年降低多少万元?
②若打算在2017年把每件产品成本降低到3.2万元,则还需要投入技改资金多少万元?(结果精确到0.01万元).
如图,以 边为直径的 经过点 , 是 上一点,连接 交 于点 ,且 , .
(1)试判断 与 的位置关系,并说明理由;
(2)若点 是弧 的中点,已知 ,求 的值.

在四边形 中, ,对角线 平分 .
(1)如图1,若 ,且 ,试探究边 、 与对角线 的数量关系并说明理由.
(2)如图2,若将(1)中的条件“ ”去掉,(1)中的结论是否成立?请说明理由.
(3)如图3,若 ,探究边 、 与对角线 的数量关系并说明理由.

如图1,抛物线 与 相交于点 、 , 与 分别交 轴于点 、 ,且 为线段 的中点.
(1)求 的值;
(2)若 ,求 的面积;
(3)抛物线 的对称轴为 ,顶点为 ,在(2)的条件下:
①点 为抛物线 对称轴 上一动点,当 的周长最小时,求点 的坐标;
②如图2,点 在抛物线 上点 与点 之间运动,四边形 的面积是否存在最大值?若存在,求出面积的最大值和点 的坐标;若不存在,请说明理由.
