下列四个数中,比 小的数是
A.0B.1C. D.
不等式 的解集是
A. B. C. D.
某微生物的直径为0.000 005 ,用科学记数法表示该数为
A. B.
C. D.
如图所示的几何体的主视图是

A. B.
B. C.
C. D.
D.
下列说法错误的是
A.给定一组数据,那么这组数据的平均数一定只有一个
B.给定一组数据,那么这组数据的中位数一定只有一个
C.给定一组数据,那么这组数据的众数一定只有一个
D.如果一组数据存在众数,那么该众数一定是这组数据中的某一个
下列运算结果正确的是
A. B.
C. D.
已知关于 , 的二元一次方程组 的解为 ,则 的值是
A. B.2C.3D.
“今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为

A.1.25尺B.57.5尺C.6.25尺D.56.5尺
如图,在 中, ,点 是内心,则 的大小为

A. B. C. D.
如图, 过 对角线的交点 ,交 于 ,交 于 ,若 的周长为18, ,则四边形 的周长为

A.14B.13C.12D.10
若一次函数 的图象过第一、三、四象限,则二次函数
A.有最大值 .B.有最大值 .C.有最小值 .D.有最小值 .
已知 ,则 的值等于
A.1B.0C. D.
分解因式: .
是等边三角形,点 是三条高的交点.若 以点 为旋转中心旋转后能与原来的图形重合,则 旋转的最小角度是 .
已知一元二次方程 的两个实数根为 , ,则 的值是 .
设点 和点 , 是直线 上的两个点,则 、 的大小关系为 .
如图, 是 的弦,半径 于点 ,且 , ,则 .

已知反比例函数 ,当 时, 的取值范围为 .
先化简,再求值: ,其中 .
解方程: .
在如图的正方形网格中,每一个小正方形的边长为1.格点三角形 (顶点是网格线交点的三角形)的顶点 、 的坐标分别是 , .
(1)请在图中的网格平面内建立平面直角坐标系;
(2)请画出 关于 轴对称的△ ;
(3)请在 轴上求作一点 ,使△ 的周长最小,并写出点 的坐标.

如图,为了测得一棵树的高度 ,小明在 处用高为 的测角仪 ,测得树顶 的仰角为 ,再向树方向前进 ,又测得树顶 的仰角为 ,求这棵树的高度 .

一个口袋中放有290个涂有红、黑、白三种颜色的质地相同的小球.若红球个数是黑球个数的2倍多40个.从袋中任取一个球是白球的概率是 .
(1)求袋中红球的个数;
(2)求从袋中任取一个球是黑球的概率.
某烘焙店生产的蛋糕礼盒分为六个档次,第一档次(即最低档次)的产品每天生产76件,每件利润10元.调查表明:生产每提高一个档次的蛋糕产品,该产品每件利润增加2元.
(1)若生产的某批次蛋糕每件利润为14元,此批次蛋糕属第几档次产品;
(2)由于生产工序不同,蛋糕产品每提高一个档次,一天产量会减少4件.若生产的某档次产品一天的总利润为1080元,该烘焙店生产的是第几档次的产品?
如图,点 是正方形 的边 延长线上一点,连接 ,过顶点 作 ,垂足为 , 分别交 于 ,交 于 .
(1)求证: ;
(2)若点 为 的中点,求 的值.

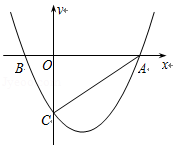
如图,抛物线 与 轴交于 、 两点,与 轴交于 点,已知 ,且 是抛物线上另一点.
(1)求 、 的值;
(2)连接 ,设点 是 轴上任一点,若以 、 、 三点为顶点的三角形是等腰三角形,求 点的坐标;
(3)若点 是 轴正半轴上且在抛物线内的一动点(不与 、 重合),过点 作 交抛物线的对称轴于 点.设 , 的面积为 ,求 与 之间的函数关系式.