的绝对值是
A. B. C.3D.
下列运算中正确的是
A. B.
C. D.
已知关于 的一元一次方程 的解为4,则 的值是
A. B.1C. D.
某小组长统计组内5人一天在课堂上的发言次数分别为3,3,0,4,5.关于这组数据,下列说法错误的是
A.众数是3B.中位数是0C.平均数3D.方差是2.8
如图是由几个相同小正方体组成的立体图形的俯视图,图上的数字表示该位置上小正方体的个数,这个立体图形的左视图是

A. B.
B.
C. D.
D.
一元一次不等式组 的最大整数解是
A. B.0C.1D.2
如图, 是正五边形 的外接圆,点 是 的一点,则 的度数是
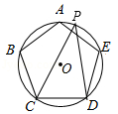
A. B. C. D.
小明和小华是同班同学,也是邻居,某日早晨,小明 先出发去学校,走了一段后,在途中停下吃了早餐,后来发现上学时间快到了,就跑步到学校;小华离家后直接乘公交汽车到了学校.如图是他们从家到学校已走的路程 (米 和所用时间 (分钟)的关系图.则下列说法中错误的是

A.小明吃早餐用时5分钟
B.小华到学校的平均速度是240米 分
C.小明跑步的平均速度是100米 分
D.小华到学校的时间是
如图为一次函数 与反比例函数 在同一坐标系中的大致图象,其中较准确的是
A. B.
B.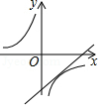
C.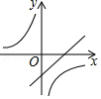 D.
D.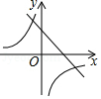
若用“ ”表示一种运算规则,我们规定: ,如: .以下说法中错误的是
A.不等式 的解集是
B.函数 的图象与 轴有两个交点
C.在实数范围内,无论 取何值,代数式 的值总为正数
D.方程 的解是
某物体质量为325000克,用科学记数法表示为 克.
一个多边形的每一个外角都是 ,这个多边形的边数为 .
如图, , , ,则 的度数为 .

如图是一块圆环形玉片的残片,作外圆的弦 与内圆相切于点 ,量得 、点 与 的中点 的距离 .则此圆环形玉片的外圆半径为 .

如图,在 中, , , ,以点 为原点建立平面直角坐标系,使 在 轴正半轴上,点 是 边上的一个动点, 交 于 , 于 , 于 .以下结论:
① ;
②当 为 的中点时, ;
③点 的坐标为 ;
④将 沿 所在的直线翻折到原来的平面,点 的对应点 的坐标为 ;
⑤矩形 的最大面积为3.在这些结论中正确的有 (只填序号)

计算: .
先化简,再求值: ,其中 .
如图,在菱形 中,过 作 于 ,过 作 于 .
求证: .

为了提高学生的身体素质,某班级决定开展球类活动,要求每个学生必须在篮球、足球、排球、乒乓球、羽毛球中选择一项参加训练(只选择一项),根据学生的报名情况制成如下统计表:
项目 |
篮球 |
足球 |
排球 |
乒乓球 |
羽毛球 |
报名人数 |
12 |
8 |
4 |
|
10 |
占总人数的百分比 |
|
|
(1)该班学生的总人数为 人;
(2)由表中的数据可知: , ;
(3)报名参加排球训练的四个人为两男(分别记为 、 两女(分别记为 、 ,现要随机在这4人中选2人参加学校组织的校级训练,请用列表或树状图的方法求出刚好选中一男一女的概率.
某报刊销售处从报社购进甲、乙两种报纸进行销售.已知从报社购进甲种报纸200份与乙种报纸300份共需360元,购进甲种报纸300份与乙种报纸200份共需340元
(1)求购进甲、乙两种报纸的单价;
(2)已知销售处卖出甲、乙两种报纸的售价分别为每份1元、1.5元.销售处每天从报社购进甲、乙两种报纸共600份,若每天能全部销售完并且销售这两种报纸的总利润不低于300元,问该销售处每天最多购进甲种报纸多少份?
如图,雨后初晴,李老师在公园散步,看见积水水面上出现梯步上方树的倒影,于是想利用倒影与物体的对称性测量这颗树的高度,他的方法是:测得树顶的仰角 、测量点 到水面平台的垂直高度 、看到倒影顶端的视线与水面交点 到 的水半距离 .再测得梯步斜坡的坡角 和长度 ,根据以下数据进行计算,
如图, 米, 米, 米, , .已知线段 和线段 关于直线 对称.(以下结果保留根号)
(1)求梯步的高度 ;
(2)求树高 .

如图,矩形 在平面直角坐标系的第一象限内, 与 轴平行, ,点 的坐标为 , 是 的中点;反比例函数 图象经过点 和点 ,过点 的直线 与反比例函数图象交于点 ,点 的纵坐标为4.
(1)求反比例函数的解析式和点 的坐标;
(2)求直线 的解析式;
(3)直接写出 时,自变量 的取值范围.

如图1, 是 的直径 上的一点,过 作 交 于 、 , 是 上的一点,过 的直线分别与 、 的延长线相交于 、 ,连接 交 于 , .
(1)求证: 是 的切线;
(2)若 , 的半径为4, ,求 的长;
(3)如图2,在(2)的条件下,连接 、 ;在线段 上有一点 ,并且以 、 、 为顶点的三角形与 相似,求 的长度.

已知抛物线的顶点为 并经过点 ,点 在抛物线的对称轴上并且纵坐标为 ,抛物线交 轴于点 .如图1.
(1)求抛物线的解析式;
(2)点 为抛物线对称轴上的一点, 为等腰三角形,求点 的坐标;
(3)如图2,点 为直线 上的一个动点,过点 的直线 与 垂直
①求证:直线 与抛物线总有两个交点;
②设直线 与抛物线交于点 、 (点 在左侧),分别过点 、 作直线 的垂线,垂足分别为 、 .求 的长.
