下列实数中,无理数是
A.0B. C. D.
下列运算结果是 的是
A. B. C. D.
如图,实数 、 、3、 在数轴上的对应点分别为 、 、 、 ,这四个数中绝对值最小的数对应的点是

A.点 B.点 C.点 D.点
如图,等腰直角三角形的顶点 、 分别在直线 、 上,若 , ,则 的度数为

A. B. C. D.
下列平面图形中,既是中心对称图形,又是轴对称图形的是
A.菱形B.等边三角形C.平行四边形D.等腰梯形
抛物线 的顶点坐标为
A. B. C. D.
若点 在第二象限,则点 在
A.第一象限B.第二象限C.第三象限D.第四象限
布袋中装有除颜色外没有其他区别的1个红球和2个白球,搅匀后从中摸出一个球,放回搅匀,再摸出第二个球,两次都摸出白球的概率是
A. B. C. D.
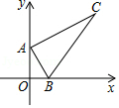
如图,点 的坐标为 ,点 是 轴正半轴上的一动点,以 为边作 ,使 , ,设点 的横坐标为 ,点 的纵坐标为 ,能表示 与 的函数关系的图象大致是
A.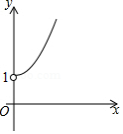 B.
B.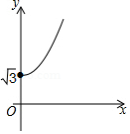
C.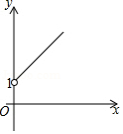 D.
D.
如图,在矩形 中, 是 边的中点,沿 对折矩形 ,使 点落在点 处,折痕为 ,连接 并延长 交 于 点,连接 并延长 交 于 点.给出以下结论:
①四边形 为平行四边形;
② ;
③ 为等腰三角形;
④ .
其中正确结论的个数为

A.1B.2C.3D.4
分解因式: .
如果 ,那么代数式 的值是 .
样本数据1,2,3,4,5.则这个样本的方差是 .
关于 的不等式 有3个正整数解,则 的取值范围是 .
如图,在矩形 中, , ,矩形内部有一动点 满足 ,则点 到 、 两点的距离之和 的最小值为 .

如图,已知点 在反比例函数 的图象上,作 ,边 在 轴上,点 为斜边 的中点,连接 并延长交 轴于点 ,若 的面积为4,则 .

解方程: .
某校为了预测本校九年级男生毕业体育测试达标情况,随机抽取该年级部分男生进行了一次测试(满分50分,成绩均记为整数分),并按测试成绩 (单位:分)分成四类: 类 , 类 , 类 , 类 绘制出如图所示的两幅不完整的统计图,请根据图中信息解答下列问题:

(1)求本次抽取的样本容量和扇形统计图中 类所对的圆心角的度数;
(2)若该校九年级男生有500名, 类为测试成绩不达标,请估计该校九年级男生毕业体育测试成绩能达标的有多少名?
攀枝花市出租车的收费标准是:起步价5元(即行驶距离不超过2千米都需付5元车费),超过2千米以后,每增加1千米,加收1.8元(不足1千米按1千米计).某同学从家乘出租车到学校,付了车费24.8元.求该同学的家到学校的距离在什么范围?
已知 中, .
(1)请在图1中作出 边上的中线(保留作图痕迹,不写作法);
(2)如图2,设 边上的中线为 ,求证: .

如图,在平面直角坐标系中, 点的坐标为 , 轴于点 , ,反比例函数 的图象的一支分别交 、 于点 、 .延长 交反比例函数的图象的另一支于点 .已知点 的纵坐标为 .
(1)求反比例函数的解析式;
(2)求直线 的解析式;
(3)求 .

如图,在 中, ,以 为直径的 分别与 、 交于点 、 ,过点 作 于点 .
(1)若 的半径为3, ,求阴影部分的面积;
(2)求证: 是 的切线;
(3)求证: .

如图,在 中, , , .动点 从 点出发,沿 方向以每秒5个单位长度的速度向 点匀速运动,动点 从 点同时出发,以相同的速度沿 方向向 点匀速运动,当点 运动到 点时, 、 两点同时停止运动,以 为边作正 、 、 按逆时针排序),以 为边在 上方作正 ,设点 运动时间为 秒.
(1)求 的值;
(2)当 与 的面积满足 时,求 的值;
(3)当 为何值时, 的某个顶点 点除外)落在 的边上.

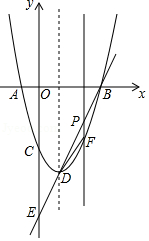
如图,对称轴为直线 的抛物线 与 轴交于 , 、 , 两点,与 轴交于 点,且 .
(1)求抛物线的解析式;
(2)抛物线顶点为 ,直线 交 轴于 点;
①设点 为线段 上一点(点 不与 、 两点重合),过点 作 轴的垂线与抛物线交于点 ,求 面积的最大值;
②在线段 上是否存在点 ,使得 ?若存在,求出点 的坐标;若不存在,请说明理由.