的值是
A. B.7C. D.10
下列等式成立的是
A. B.
C. D.
二元一次方程组 的解是
A. B. C. D.
下列说法正确的是
A.有两条边和一个角对应相等的两个三角形全等
B.正方形既是轴对称图形又是中心对称图形
C.矩形的对角线互相垂直平分
D.六边形的内角和是
如图,5个完全相同的小正方体组成了一个几何体,则这个几何体的主视图是

A. B.
B.
C. D.
D.
已知圆锥的母线长为6,将其侧面沿着一条母线展开后所得扇形的圆心角为 ,则该扇形的面积是
A. B. C. D.
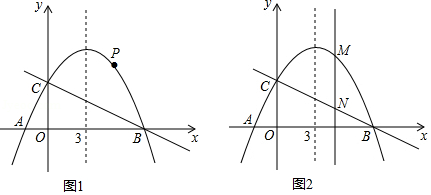
已知一次函数 与反比例函数 的图象如图所示,则当 时,自变量 满足的条件是

A. B. C. D.
如图,在 中, 是直径,半径 垂直于弦 于 ,连接 ,若 , ,则 的长是

A.5B.6C.7D.8
已知二次函数 的图象如图所示,则以下结论同时成立的是

A. B.
C. D.
已知如图,在正方形 中, , , 分别是 , 上的一点,且 , ,将 绕点 沿顺时针方向旋转 后与 重合,连接 ,过点 作 ,交 于点 ,则以下结论:① ,② ,③ ,④ 中正确的是

A.①②③B.②③④C.①③④D.①②④
分解因式 .
已知一组数据:12,10,8,15,6,8.则这组数据的中位数是 .
已知反比例函数 的图象过点 ,则当 时, 随 的增大而 .
, 两市相距200千米,甲车从 市到 市,乙车从 市到 市,两车同时出发,已知甲车速度比乙车速度快15千米 小时,且甲车比乙车早半小时到达目的地.若设乙车的速度是 千米 小时,则根据题意,可列方程 .
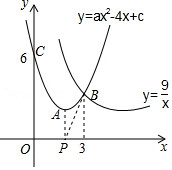
如图,已知抛物线 与反比例函数 的图象相交于点 ,且 点的横坐标为3,抛物线与 轴交于点 , 是抛物线 的顶点, 点是 轴上一动点,当 最小时, 点的坐标为 .
计算: .
先化简,再求值 .(其中 ,
如图,在 中, , 分别是 , 上的点,且 , .求证:四边形 是菱形.

已知关于 的一元二次方程 的两实数根 , 满足 ,求 的取值范围.
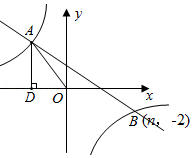
如图所示,在平面直角坐标系中,一次函数 与反比例函数 的图象交于第二、四象限 、 两点,过点 作 轴于 , , ,且点 的坐标为 .
(1)求一次函数与反比例函数的解析式;
(2) 是 轴上一点,且 是等腰三角形,请直接写出所有符合条件的 点坐标.
如图,过 外一点 作 的切线 切 于点 ,连接 并延长,与 交于 、 两点, 是半圆 的中点,连接 交 于点 ,连接 、 .
(1)求证: ;
(2)若 , ,求 的长.

请阅读以下材料:已知向量 , , , 满足下列条件:
① ,
② (角 的取值范围是 ;
③
利用上述所给条件解答问题:
如:已知 , , ,求角 的大小;
解: ,
又
,
角 的值为 .
请仿照以上解答过程,完成下列问题:
已知 , ,求角 的大小.
学习习近平总书记关于生态文明建设重要讲话,牢固树立“绿水青山就是金山银山”的科学观,让环保理念深入到学校,某校张老师为了了解本班学生3月植树成活情况,对本班全体学生进行了调查,并将调查结果分为了三类: :好, :中, :差.
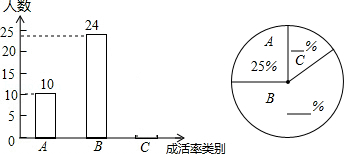
请根据图中信息,解答下列问题:
(1)求全班学生总人数;
(2)将上面的条形统计图与扇形统计图补充完整;
(3)张老师在班上随机抽取了4名学生,其中 类1人, 类2人, 类1人,若再从这4人中随机抽取2人,请用画树状图或列表法求出全是 类学生的概率.
如图,某测量小组为了测量山 的高度,在地面 处测得山顶 的仰角 ,然后沿着坡度为 的坡面 走了200米达到 处,此时在 处测得山顶 的仰角为 ,求山高 (结果保留根号).

如图,已知抛物线 的对称轴是直线 ,且与 轴相交于 , 两点 点在 点右侧)与 轴交于 点.
(1)求抛物线的解析式和 、 两点的坐标;
(2)若点 是抛物线上 、 两点之间的一个动点(不与 、 重合),则是否存在一点 ,使 的面积最大.若存在,请求出 的最大面积;若不存在,试说明理由;
(3)若 是抛物线上任意一点,过点 作 轴的平行线,交直线 于点 ,当 时,求 点的坐标.