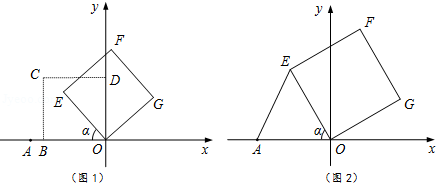实数 的绝对值是
A.2B. C. D.
若实数 , 在数轴上的位置如图所示,则下列判断错误的是

A. B. C. D. , 互为倒数
如图是加工零件的尺寸要求,现有下列直径尺寸的产品(单位: ,其中不合格的是

A. B. C. D.
从一个边长为 的大立方体挖去一个边长为 的小立方体,得到的几何体如图所示,则该几何体的左视图正确的是

A. B.
B. C.
C. D.
D.
一元二次方程 的两根为 , ,则下列结论正确的是
A . , B . , C . D .
如图,已知 ,添加下列条件还不能判定 的是

A. B. C. D.
小明和小华参加社会实践活动,随机选择“打扫社区卫生”和“参加社会调查”其中一项,那么两人同时选择“参加社会调查”的概率为
A. B. C. D.
一座楼梯的示意图如图所示, 是铅垂线, 是水平线, 与 的夹角为 .现要在楼梯上铺一条地毯,已知 米,楼梯宽度1米,则地毯的面积至少需要

A. 米 B. 米 C. 米 D. 米
足球射门,不考虑其他因素,仅考虑射点到球门 的张角大小时,张角越大,射门越好.如图的正方形网格中,点 , , , , 均在格点上,球员带球沿 方向进攻,最好的射点在
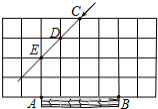
A.点 B.点 或点
C.线段 (异于端点) 上一点D.线段 (异于端点) 上一点
在四边形 中, , , , 垂直平分 ,点 为垂足.设 , ,则 关于 的函数关系用图象大致可以表示为
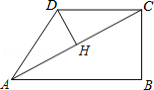
A.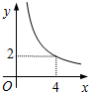 B.
B.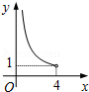
C.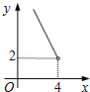 D.
D.
不等式 的解集是 .
能够说明“ 不成立”的 的值是 (写出一个即可).
为监测某河道水质,进行了6次水质检测,绘制了如图的氨氮含量的折线统计图.若这6次水质检测氨氮含量平均数为 ,则第3次检测得到的氨氮含量是 .

如图,已知 , .若 , ,则 的度数是 .
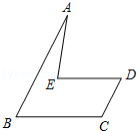
如图, 纸片中, , , ,点 在边 上,以 为折痕 折叠得到△ , 与边 交于点 .若 为直角三角形,则 的长是 .

由6根钢管首尾顺次铰接而成六边形钢架 ,相邻两钢管可以转动.已知各钢管的长度为 米, 米.(铰接点长度忽略不计)
(1)转动钢管得到三角形钢架,如图1,则点 , 之间的距离是 米.
(2)转动钢管得到如图2所示的六边形钢架,有 ,现用三根钢条连接顶点使该钢架不能活动,则所用三根钢条总长度的最小值是 米.

计算: .
解方程组 .
某校组织学生排球垫球训练,训练前后,对每个学生进行考核.现随机抽取部分学生,统计了训练前后两次考核成绩,并按“ , , ”三个等次绘制了如图不完整的统计图.试根据统计图信息,解答下列问题:
(1)抽取的学生中,训练后“ ”等次的人数是多少?并补全统计图.
(2)若学校有600名学生,请估计该校训练后成绩为“ ”等次的人数.

如图1表示同一时刻的韩国首尔时间和北京时间,两地时差为整数.
(1)设北京时间为 (时 ,首尔时间为 (时 ,就 ,求 关于 的函数表达式,并填写下表(同一时刻的两地时间).
北京时间 |
|
|
|
首尔时间 |
|
|
|
(2)如图2表示同一时刻的英国伦敦时间(夏时制)和北京时间,两地时差为整数.如果现在伦敦(夏时制)时间为 ,那么此时韩国首尔时间是多少?

如图,直线 与 , 轴分别交于点 , ,与反比例函数 图象交于点 , ,过点 作 轴的垂线交该反比例函数图象于点 .
(1)求点 的坐标.
(2)若 .
①求 的值.
②试判断点 与点 是否关于原点 成中心对称?并说明理由.

四边形 的对角线交于点 ,有 , ,以 为直径的半圆过点 ,圆心为 .
(1)利用图1,求证:四边形 是菱形.
(2)如图2,若 的延长线与半圆相切于点 ,已知直径 .
①连接 ,求 的面积.
②求弧 的长.

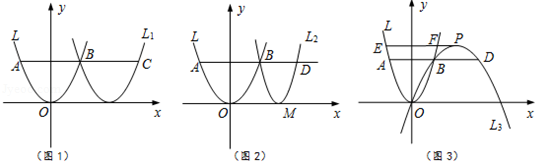
在平面直角坐标系中,点 为原点,平行于 轴的直线与抛物线 相交于 , 两点(点 在第一象限),点 在 的延长线上.
(1)已知 ,点 的纵坐标为2.
①如图1,向右平移抛物线 使该抛物线过点 ,与 的延长线交于点 ,求 的长.
②如图2,若 ,过点 , 的抛物线 ,其顶点 在 轴上,求该抛物线的函数表达式.
(2)如图3,若 ,过 , , 三点的抛物线 ,顶点为 ,对应函数的二次项系数为 ,过点 作 轴,交抛物线 于 , 两点,求 的值,并直接写出 的值.
在平面直角坐标系中,点 为原点,点 的坐标为 .如图1,正方形 的顶点 在 轴的负半轴上,点 在第二象限.现将正方形 绕点 顺时针旋转角 得到正方形 .
(1)如图2,若 , ,求直线 的函数表达式.
(2)若 为锐角, ,当 取得最小值时,求正方形 的面积.
(3)当正方形 的顶点 落在 轴上时,直线 与直线 相交于点 , 的其中两边之比能否为 ?若能,求点 的坐标;若不能,试说明理由