在数1,0, , 中,最大的数是
A. B. C.0D.1
计算 的正确结果是
A. B. C. D.
如图是底面为正方形的长方体,下面有关它的三个视图的说法正确的是

A.俯视图与主视图相同B.左视图与主视图相同
C.左视图与俯视图相同D.三个视图都相同
根据 空气质量标准:24小时 均值在 (微克 立方米)的空气质量等级为优.将环保部门对我市 一周的检测数据制作成如下统计表,这组 数据的中位数是
天数 |
3 |
1 |
1 |
1 |
1 |
|
18 |
20 |
21 |
29 |
30 |
A.21微克 立方米B.20微克 立方米
C.19微克 立方米D.18微克 立方米
化简 的结果是
A. B. C. D.
若关于 的一元一次方程 的解是负数,则 的取值范围是
A. B. C. D.
如图,在 中,连接 , , ,则 的长是
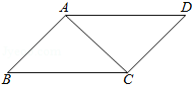
A. B.2C. D.4
将函数 的图象用下列方法平移后,所得的图象不经过点 的方法是
A.向左平移1个单位B.向右平移3个单位
C.向上平移3个单位D.向下平移1个单位
如图,点 是以 为直径的半圆 的三等分点, ,则图中阴影部分的面积是
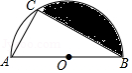
A. B. C. D.
在同一条道路上,甲车从 地到 地,乙车从 地到 地,乙先出发,图中的折线段表示甲、乙两车之间的距离 (千米)与行驶时间 (小时)的函数关系的图象,下列说法错误的是

A.乙先出发的时间为0.5小时
B.甲的速度是80千米 小时
C.甲出发0.5小时后两车相遇
D.甲到 地比乙到 地早 小时
分解因式: .
等腰三角形的一个内角为 ,则顶角的度数是 .
已知 ,则代数式 的值为 .
如图,由6个小正方形组成的 网格中,任意选取5个小正方形并涂黑,则黑色部分的图形是轴对称图形的概率是 .

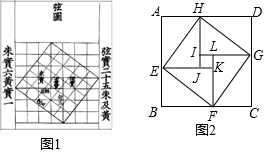
我国三国时期数学家赵爽为了证明勾股定理,创造了一幅“弦图”,后人称其为“赵爽弦图”,如图1所示.在图2中,若正方形 的边长为14,正方形 的边长为2,且 ,则正方形 的边长为 .
如图,在平面直角坐标系 中,直线 分别交 轴, 轴于 , 两点,已知点 .
(1)当直线 经过点 时,点 到直线 的距离是 ;
(2)设点 为线段 的中点,连接 , ,若 ,则 的值是 .

计算: .
解方程: .
如图是某小区的一个健身器材,已知 , , ,求端点 到地面 的距离(精确到 .(参考数据: , ,

在全体丽水人民的努力下,我市剿灭劣 类水“河道清淤”工程取得了阶段性成果,如表是全市十个县(市、区)指标任务数的统计表;如图是截止2017年3月31日和截止5月4日,全市十个县(市、区)指标任务累计完成数的统计图.

全市十个县(市、区)指标任务数统计表
县(市、区) |
任务数(万方) |
|
25 |
|
25 |
|
20 |
|
12 |
|
13 |
|
25 |
|
16 |
|
25 |
|
11 |
|
28 |
合计 |
200 |
(1)截止3月31日,完成进度(完成进度 累计完成数 任务数 最快、最慢的县(市、区)分别是哪一个?
(2)求截止5月4日全市的完成进度;
(3)请结合图表信息和数据分析,对Ⅰ县完成指标任务的行动过程和成果进行评价.
丽水某公司将“丽水山耕”农副产品运往杭州市场进行销售,记汽车行驶时间为 小时,平均速度为 千米 小时(汽车行驶速度不超过100千米 小时).根据经验, , 的一组对应值如下表:
(千米 小时) |
75 |
80 |
85 |
90 |
95 |
(小时) |
4.00 |
3.75 |
3.53 |
3.33 |
3.16 |
(1)根据表中的数据,求出平均速度 (千米 小时)关于行驶时间 (小时)的函数表达式;
(2)汽车上午 从丽水出发,能否在上午 之前到达杭州市场?请说明理由;
(3)若汽车到达杭州市场的行驶时间 满足 ,求平均速度 的取值范围.
如图,在 中, ,以 为直径的 交 于点 ,切线 交 于点 .
(1)求证: ;
(2)若 , ,求 的长.

如图1,在 中, ,点 从点 出发以 的速度沿折线 运动,点 从点 出发以 的速度沿 运动, , 两点同时出发,当某一点运动到点 时,两点同时停止运动.设运动时间为 , 的面积为 , 关于 的函数图象由 , 两段组成,如图2所示.

(1)求 的值;
(2)求图2中图象 段的函数表达式;
(3)当点 运动到线段 上某一段时 的面积,大于当点 在线段 上任意一点时 的面积,求 的取值范围.
如图,在矩形 中,点 是 上的一个动点,连接 ,作点 关于 的对称点 ,且点 落在矩形 的内部,连接 , , ,过点 作 交 于点 ,设 .
(1)求证: ;
(2)当点 落在 上时,用含 的代数式表示 的值;
(3)若 ,且以点 , , 为顶点的三角形是直角三角形,求 的值.
