的相反数为
A. B. C. D.3
地球与太阳的平均距离大约为 .将150000000用科学记数法表示应为
A. B. C. D.
若一组数据3、4、5、 、6、7的平均数是5,则 的值是
A.4B.5C.6D.7
若点 在反比例函数 的图象上,则 的值是
A. B. C.2D.6
如图,三角板的直角顶点落在矩形纸片的一边上.若 ,则 的度数是

A. B. C. D.
如图,菱形 的对角线 、 的长分别为6和8,则这个菱形的周长是

A.20B.24C.40D.48
若关于 的一元二次方程 有两个相等的实数根,则 的值是
A. B.0C.1D.2
如图,点 、 、 都在 上,若 ,则 的度数是
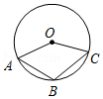
A. B. C. D.
.
一元二次方程 的根是 .
某射手在相同条件下进行射击训练,结果如下:
射击次数 |
10 |
20 |
40 |
50 |
100 |
200 |
500 |
1000 |
击中靶心的频数 |
9 |
19 |
37 |
45 |
89 |
181 |
449 |
901 |
击中靶心的频率 |
0.900 |
0.950 |
0.925 |
0.900 |
0.890 |
0.905 |
0.898 |
0.901 |
该射手击中靶心的概率的估计值是 (精确到 .
若关于 、 的二元一次方程 有一个解是 ,则 .
若一个等腰三角形的顶角等于 ,则它的底角等于 .
将二次函数 的图象向上平移3个单位长度,得到的图象所对应的函数表达式是 .
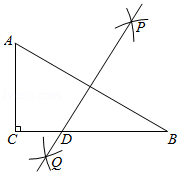
如图,在 中, , , ,分别以点 、 为圆心,大于 的长为半径画弧,两弧交点分别为点 、 ,过 、 两点作直线交 于点 ,则 的长是 .
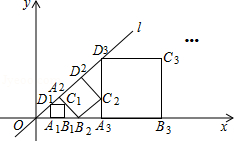
如图,在平面直角坐标系中,直线 为正比例函数 的图象,点 的坐标为 ,过点 作 轴的垂线交直线 于点 ,以 为边作正方形 ;过点 作直线 的垂线,垂足为 ,交 轴于点 ,以 为边作正方形 ;过点 作 轴的垂线,垂足为 ,交直线 于点 ,以 为边作正方形 , ,按此规律操作下所得到的正方形 的面积是 .
(1)计算: ;
(2)解不等式组:
先化简,再求值: ,其中 .
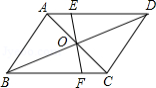
已知:如图, 的对角线 、 相交于点 ,过点 的直线分别与 、 相交于点 、 .求证: .
某学校为了解学生上学的交通方式,现从全校学生中随机抽取了部分学生进行“我上学的交通方式”问卷调查,规定每人必须并且只能在“乘车”、“步行”、“骑车”和“其他”四项中选择一项,并将统计结果绘制了如下两幅不完整的统计图.
请解答下列问题:
(1)在这次调查中,该学校一共抽样调查了 名学生;
(2)补全条形统计图;
(3)若该学校共有1500名学生,试估计该学校学生中选择“步行”方式的人数.

一只不透明袋子中装有三只大小、质地都相同的小球,球面上分别标有数字1、 、3,搅匀后先从中任意摸出一个小球(不放回),记下数字作为点 的横坐标,再从余下的两个小球中任意摸出一个小球,记下数字作为点 的纵坐标.
(1)用画树状图或列表等方法列出所有可能出现的结果;
(2)求点 落在第四象限的概率.
如图,在平面直角坐标系中,一次函数 的图象经过点 ,且与 轴相交于点 ,与正比例函数 的图象相交于点 ,点 的横坐标为1.
(1)求 、 的值;
(2)若点 在 轴负半轴上,且满足 ,求点 的坐标.

为了计算湖中小岛上凉亭 到岸边公路 的距离,某数学兴趣小组在公路 上的点 处,测得凉亭 在北偏东 的方向上;从 处向正东方向行走200米,到达公路 上的点 处,再次测得凉亭 在北偏东 的方向上,如图所示.求凉亭 到公路 的距离.(结果保留整数,参考数据: ,

如图, 是 的直径, 是 的切线,切点为 , 交 于点 ,点 是 的中点.
(1)试判断直线 与 的位置关系,并说明理由;
(2)若 的半径为2, , ,求图中阴影部分的面积.

某景区商店销售一种纪念品,每件的进货价为40元.经市场调研,当该纪念品每件的销售价为50元时,每天可销售200件;当每件的销售价每增加1元,每天的销售数量将减少10件.
(1)当每件的销售价为52元时,该纪念品每天的销售数量为 件;
(2)当每件的销售价 为多少时,销售该纪念品每天获得的利润 最大?并求出最大利润.
如果三角形的两个内角 与 满足 ,那么我们称这样的三角形为“准互余三角形”.
(1)若 是“准互余三角形”, , ,则 ;
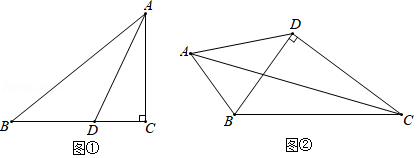
(2)如图①,在 中, , , .若 是 的平分线,不难证明 是“准互余三角形”.试问在边 上是否存在点 (异于点 ,使得 也是“准互余三角形”?若存在,请求出 的长;若不存在,请说明理由.
(3)如图②,在四边形 中, , , , ,且 是“准互余三角形”,求对角线 的长.
如图,在平面直角坐标系中,一次函数 的图象与 轴和 轴分别相交于 、 两点.动点 从点 出发,在线段 上以每秒3个单位长度的速度向点 作匀速运动,到达点 停止运动,点 关于点 的对称点为点 ,以线段 为边向上作正方形 .设运动时间为 秒.
(1)当 秒时,点 的坐标是 ;
(2)在运动过程中,设正方形 与 重叠部分的面积为 ,求 与 的函数表达式;
(3)若正方形 对角线的交点为 ,请直接写出在运动过程中 的最小值.
