的相反数是
A . B . C . 8D .
下列运算正确的是
A. B.
C. D.
地球上陆地的面积约为150 000 .把“150 000 000”用科学记数法表示为
A. B. C. D.
一组数据2,1,2,5,3,2的众数是
A.1B.2C.3D.5
如图,任意转动正六边形转盘一次,当转盘停止转动时,指针指向大于3的数的概率是

A. B. C. D.
如图是由5个大小相同的正方体搭成的几何体,这个几何体的俯视图是

A. B.
B.
C. D.
D.
已知学校航模组设计制作的火箭的升空高度 与飞行时间 满足函数表达式 .则下列说法中正确的是
A.点火后 和点火后 的升空高度相同
B.点火后 火箭落于地面
C.点火后 的升空高度为
D.火箭升空的最大高度为
如图,菱形 的两个顶点 、 在反比例函数 的图象上,对角线 与 的交点恰好是坐标原点 ,已知点 , ,则 的值是

A. B. C. D.
使 有意义的 的取值范围是 .
分解因式: .
如图, 中,点 、 分别在 、 上, , ,则 与 的面积的比为 .

已知 , 是反比例函数 图象上的两个点,则 与 的大小关系为 .
一个扇形的圆心角是 .它的半径是 .则扇形的弧长为 .
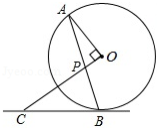
如图, 是 的弦,点 在过点 的切线上,且 , 交 于点 ,已知 ,则 .
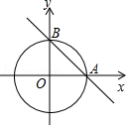
如图,一次函数 的图象与 轴、 轴分别相交于 、 两点, 经过 , 两点,已知 ,则 的值为 .
如图, 、 , 、 分别为矩形 的边 、 、 、 的中点,连接 、 、 , , .已知 , ,则 的长为 .

计算: .
解方程: .
解不等式组:
随着我国经济社会的发展,人民对于美好生活的追求越来越高.某社区为了了解家庭对于文化教育的消费情况,随机抽取部分家庭,对每户家庭的文化教育年消费金额进行问卷调查,根据调查结果绘制成两幅不完整的统计图表.
请你根据统计图表提供的信息,解答下列问题:
(1)本次被调查的家庭有 户,表中 ;
(2)本次调查数据的中位数出现在 组.扇形统计图中, 组所在扇形的圆心角是 度;
(3)这个社区有2500户家庭,请你估计家庭年文化教育消费10000元以上的家庭有多少户?
组别 |
家庭年文化教育消费金额 (元 |
户数 |
|
|
36 |
|
|
|
|
|
27 |
|
|
15 |
|
|
30 |

汤姆斯杯世界男子羽毛球团体赛小组赛比赛规则:两队之间进行五局比赛,其中三局单打,两局双打,五局比赛必须全部打完,赢得三局及以上的队获胜.假如甲,乙两队每局获胜的机会相同.
(1)若前四局双方战成 ,那么甲队最终获胜的概率是 ;
(2)现甲队在前两局比赛中已取得 的领先,那么甲队最终获胜的概率是多少?
如图,矩形 中, 是 的中点,延长 , 交于点 ,连接 , .
(1)求证:四边形 是平行四边形;
(2)当 平分 时,写出 与 的数量关系,并说明理由.

如图,在平面直角坐标系中,一次函数 的图象与反比例函数 的图象交于 、 两点,与 轴交于点 .
(1)求 , 的值;
(2)请直接写出不等式 的解集;
(3)将 轴下方的图象沿 轴翻折,点 落在点 处,连接 , ,求△ 的面积.

某村在推进美丽乡村活动中,决定建设幸福广场,计划铺设相同大小规格的红色和蓝色地砖.经过调查.获取信息如下:
购买数量低于5000块 |
购买数量不低于5000块 |
|
红色地砖 |
原价销售 |
以八折销售 |
蓝色地砖 |
原价销售 |
以九折销售 |
如果购买红色地砖4000块,蓝色地砖6000块,需付款86000元;如果购买红色地砖10000块,蓝色地砖3500块,需付款99000元.
(1)红色地砖与蓝色地砖的单价各多少元?
(2)经过测算,需要购置地砖12000块,其中蓝色地砖的数量不少于红色地砖的一半,并且不超过6000块,如何购买付款最少?请说明理由.
如图1,水坝的横截面是梯形 , ,坝顶 ,背水坡 的坡度 (即 为 ,坝底 .

(1)求坝高;
(2)如图2,为了提高堤坝的防洪抗洪能力,防汛指挥部决定在背水坡将坝顶和坝底同时拓宽加固,使得 , ,求 的长.(参考数据: , ,
如图1,图形 是由两个二次函数 与 的部分图象围成的封闭图形.已知 、 、 .
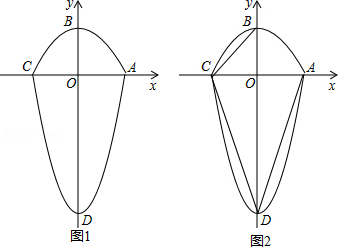
(1)直接写出这两个二次函数的表达式;
(2)判断图形 是否存在内接正方形(正方形的四个顶点在图形 上),并说明理由;
(3)如图2,连接 , , ,在坐标平面内,求使得 与 相似(其中点 与点 是对应顶点)的点 的坐标.
在数学兴趣小组活动中,小亮进行数学探究活动. 是边长为2的等边三角形, 是 上一点,小亮以 为边向 的右侧作等边三角形 ,连接 .
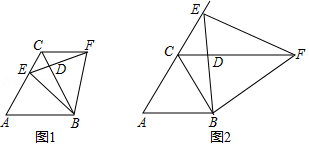
(1)如图1,当点 在线段 上时, 、 相交于点 ,小亮发现有两个三角形全等,请你找出来,并证明.
(2)当点 在线段 上运动时,点 也随着运动,若四边形 的面积为 ,求 的长.
(3)如图2,当点 在 的延长线上运动时, 、 相交于点 ,请你探求 的面积 与 的面积 之间的数量关系.并说明理由.
(4)如图2,当 的面积 时,求 的长.