中国是最早采用正负数表示相反意义的量的国家.某仓库运进面粉7吨,记为 吨,那么运出面粉8吨应记为 吨.
如图,直线 与直线 、 都相交.若 , ,则 度.

要使 有意义,则 的取值范围是 .
已知一个反比例函数的图象经过点 ,若该反比例函数的图象也经过点 ,则 .
若关于 的一元二次方程 有两个相等的实数根,则实数 的值为 .
已知四边形 是矩形,点 是矩形 的边上的点,且 .若 , ,则 的长是 .
千百年来的绝对贫困即将消除,云南省 的贫困人口脱贫, 的贫困村出列, 的贫困县摘帽,1500000人通过异地扶贫搬迁实现“挪穷窝”,“斩穷根”(摘自2020年5月11日云南日报).1500000这个数用科学记数法表示为
A. B. C. D.
下列几何体中,主视图是长方形的是
A. B.
B.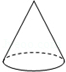
C.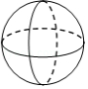 D.
D.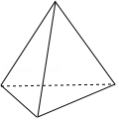
下列运算正确的是
A. B.
C. D.
下列说法正确的是
A.为了解三名学生的视力情况,采用抽样调查
B.任意画一个三角形,其内角和是 是必然事件
C.甲、乙两名射击运动员10次射击成绩(单位:环)的平均数分别为 、 ,方差分别为 、 ,若 , , ,则甲的成绩比乙的稳定
D.一个抽奖活动中,中奖概率为 ,表示抽奖20次就有1次中奖
如图,平行四边形 的对角线 , 相交于点 , 是 的中点.则 与 的面积的比等于

A. B. C. D.
按一定规律排列的单项式: , , , , , , ,第 个单项式是
A. B. C. D.
如图,正方形 的边长为4,以点 为圆心, 为半径,画圆弧 得到扇形 (阴影部分,点 在对角线 上).若扇形 正好是一个圆锥的侧面展开图,则该圆锥的底面圆的半径是

A. B.1C. D.
若整数 使关于 的不等式组 ,有且只有45个整数解,且使关于 的方程 的解为非正数,则 的值为
A. 或 B. 或
C. 或 D. 或 或
先化简,再求值: ,其中 .
如图,已知 , .求证: .

某公司员工的月工资如下:
员工 |
经理 |
副经理 |
职员 |
职员 |
职员 |
职员 |
职员 |
职员 |
杂工 |
月工资 元 |
7000 |
4400 |
2400 |
2000 |
1900 |
1800 |
1800 |
1800 |
1200 |

经理、职员 、职员 从不同的角度描述了该公司员工的收入情况.
设该公司员工的月工资数据(见上述表格)的平均数、中位数、众数分别为 、 、 ,请根据上述信息完成下列问题:
(1) , , ;
(2)上月一个员工辞职了,从本月开始,停发该员工工资,若本月该公司剩下的8名员工的月工资不变,但这8名员工的月工资数据(单位:元)的平均数比原9名员工的月工资数据(见上述表格)的平均数减小了.你认为辞职的那名员工可能是 .
某地响应“把绿水青山变成金山银山,用绿色杠杆撬动经济转型”发展理念,开展“美化绿色城市”活动,绿化升级改造了总面积为360万平方米的区域.实际施工中,由于采用了新技术,实际平均每年绿化升级改造的面积是原计划平均每年绿化升级改造的面积的2倍,所以比原计划提前4年完成了上述绿化升级改造任务.实际平均每年绿化升级改造的面积是多少万平方米?
甲、乙两个家庭来到以“生态资源,绿色旅游”为产业的美丽云南,各自随机选择到大理、丽江、西双版纳三个城市中的一个城市旅游.假设这两个家庭选择到哪个城市旅游不受任何因素影响,上述三个城市中的每一个被选到的可能性相同,甲、乙两个家庭选择到上述三个城市中的同一个城市旅游的概率为 .
(1)直接写出甲家庭选择到大理旅游的概率;
(2)用列表法或树状图法(树状图也称树形图)中的一种方法,求 的值.
如图, 为 的直径, 为 上一点, ,垂足为 , 平分 .
(1)求证: 是 的切线;
(2)若 , ,求 的长.

众志成城抗疫情,全国人民在行动.某公司决定安排大、小货车共20辆,运送260吨物资到 地和 地,支援当地抗击疫情.每辆大货车装15吨物资,每辆小货车装10吨物资,这20辆货车恰好装完这批物资.已知这两种货车的运费如下表:
目的地 车型 |
地(元 辆) |
地(元 辆) |
大货车 |
900 |
1000 |
小货车 |
500 |
700 |
现安排上述装好物资的20辆货车(每辆大货车装15吨物资,每辆小货车装10吨物资)中的10辆前往 地,其余前往 地,设前往 地的大货车有 辆,这20辆货车的总运费为 元.
(1)这20辆货车中,大货车、小货车各有多少辆?
(2)求 与 的函数解析式,并直接写出 的取值范围;
(3)若运往 地的物资不少于140吨,求总运费 的最小值.
如图,四边形 是菱形,点 为对角线 的中点,点 在 的延长线上, ,垂足为 ,点 在 的延长线上, ,垂足为 ,
(1)若 ,求证:四边形 是菱形;
(2)若 , 的面积为16,求菱形 的面积.
抛物线 与 轴交于 、 两点,与 轴交于点 ,点 的坐标为 ,点 的坐标为 .点 为抛物线 上的一个动点.过点 作 轴于点 ,交直线 于点 .
(1)求 、 的值;
(2)设点 在抛物线 的对称轴上,当 的周长最小时,直接写出点 的坐标;
(3)在第一象限,是否存在点 ,使点 到直线 的距离是点 到直线 的距离的5倍?若存在,求出点 所有的坐标;若不存在,请说明理由.