下列各式正确的是
A. B. C. D.
如图, ,点 为 上一点, 是 的平分线,若 ,则 的大小为
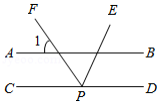
A. B. C. D.
冠状病毒的直径约为 纳米,1纳米 米,若用科学记数法表示110纳米,则正确的结果是
A. 米B. 米C. 米D. 米
在平面直角坐标系的第四象限内有一点 ,到 轴的距离为4,到 轴的距离为5,则点 的坐标为
A. B. C. D.
下列图形:线段、等边三角形、平行四边形、圆,其中既是轴对称图形,又是中心对称图形的个数为
A.1B.2C.3D.4
如图,点 在双曲线 上,点 在双曲线 上,且 轴,点 、 在 轴上,若四边形 为矩形,则它的面积为

A.4B.6C.8D.12
下列命题是假命题的是
A.对角线互相垂直且相等的平行四边形是正方形
B.对角线互相垂直的矩形是正方形
C.对角线相等的菱形是正方形
D.对角线互相垂直且平分的四边形是正方形
已知一组数据:5,4,3,4,9,关于这组数据的下列描述:
①平均数是5,②中位数是4,③众数是4,④方差是4.4,
其中正确的个数为
A.1B.2C.3D.4
在 中,直径 ,弦 于点 ,若 ,则 的长为
A.6B.9C.12D.15
对于任意实数 ,关于 的方程 的根的情况为
A.有两个相等的实数根B.没有实数根
C.有两个不相等的实数根D.无法判定
对称轴为直线 的抛物线 、 、 为常数,且 如图所示,小明同学得出了以下结论:① ,② ,③ ,④ ,⑤ 为任意实数),⑥当 时, 随 的增大而增大.其中结论正确的个数为

A.3B.4C.5D.6
如图,对折矩形纸片 ,使 与 重合,得到折痕 ,把纸片展平后再次折叠,使点 落在 上的点 处,得到折痕 , 与 相交于点 .若直线 交直线 于点 , , ,则 的长为
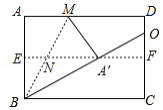
A. B. C. D.
若二次根式 在实数范围内有意义,则 的取值范围为 .
在等腰 中, , ,则 的大小为 .
若正比例函数 的图象与某反比例函数的图象有一个交点的纵坐标是2,则该反比例函数的解析式为 .
如图, 是正方形 的内切圆,切点分别为 、 、 、 , 与 相交于点 ,则 的值为 .

现有下列长度的五根木棒:3,5,8,10,13,从中任取三根,可以组成三角形的概率为 .
若关于 的不等式组 无解,则 的取值范围为 .
观察下列各式: , , , , , ,根据其中的规律可得 (用含 的式子表示).
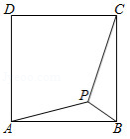
如图,点 是正方形 内一点,且点 到点 、 、 的距离分别为 、 、4,则正方形 的面积为 .
先化简,再求值: ;其中 , .
如图,在平面直角坐标系中,直线 与直线 相交于点 ,并分别与 轴相交于点 、 .
(1)求交点 的坐标;
(2)求 的面积;
(3)请把图象中直线 在直线 上方的部分描黑加粗,并写出此时自变量 的取值范围.
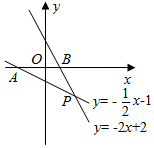
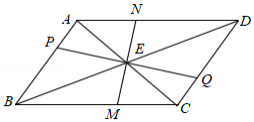
如图,过 对角线 与 的交点 作两条互相垂直的直线,分别交边 、 、 、 于点 、 、 、 .
(1)求证: ;
(2)顺次连接点 、 、 、 ,求证:四边形 是菱形.
某水果商店销售一种进价为40元 千克的优质水果,若售价为50元 千克,则一个月可售出500千克;若售价在50元 千克的基础上每涨价1元,则月销售量就减少10千克.
(1)当售价为55元 千克时,每月销售水果多少千克?
(2)当月利润为8750元时,每千克水果售价为多少元?
(3)当每千克水果售价为多少元时,获得的月利润最大?
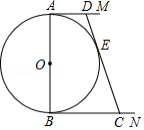
如图, 是 的直径, 和 是它的两条切线,过 上一点 作直线 ,分别交 、 于点 、 ,且 .
(1)求证:直线 是 的切线;
(2)求证: .
如图,抛物线的顶点为 ,与 轴交于点 ,点 为其对称轴上的一个定点.
(1)求这条抛物线的函数解析式;
(2)已知直线 是过点 且垂直于 轴的定直线,若抛物线上的任意一点 到直线 的距离为 ,求证: ;
(3)已知坐标平面内的点 ,请在抛物线上找一点 ,使 的周长最小,并求此时 周长的最小值及点 的坐标.
