下列各数中,绝对值最小的数是
A. B. C. D.
函数 的自变量 的取值范围是
A. B. 且 C. D. 且
在平面直角坐标系中,将点 向右平移3个单位得到点 ,则点 关于 轴的对称点的坐标为
A. B. C. D.
一个几何体由大小相同的小立方块搭成,它的俯视图如图所示,其中小正方形中的数字表示在该位置小立方块的个数,则该几何体的主视图为

A. B.
B. C.
C. D.
D.
如果顺次连接四边形的各边中点得到的四边形是矩形,那么原来四边形的对角线一定满足的条件是
A.互相平分B.相等C.互相垂直D.互相垂直平分
如图,将 绕点 顺时针旋转角 ,得到 ,若点 恰好在 的延长线上,则 等于

A. B. C. D.
等腰三角形的一边长是3,另两边的长是关于 的方程 的两个根,则 的值为
A.3B.4C.3或4D.7
一次函数 与二次函数 在同一平面直角坐标系中的图象可能是
A. B.
B.
C. D.
D.
计算 的结果是 .
方程 的解是 .
如图,在 中, ,点 为 边的中点,连接 ,若 , ,则 的值为 .

从 ,2, ,4这四个数中任取两个不同的数分别作为 , 的值,得到反比例函数 ,则这些反比例函数中,其图象在二、四象限的概率是 .
如图,在菱形 中, 是对角线, , 与边 相切于点 ,则图中阴影部分的面积为 .
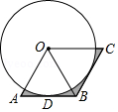
如图,矩形 中, , ,点 在对角线 上,且 ,连接 并延长,交 的延长线于点 ,连接 ,则 的长为 .

计算: .
先化简,再求值: ,其中 满足 .
如图,在 中, ,点 在 的延长线上, 于点 ,若 ,求证: .
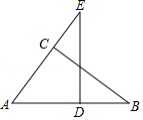
某兴趣小组为了测量大楼 的高度,先沿着斜坡 走了52米到达坡顶点 处,然后在点 处测得大楼顶点 的仰角为 ,已知斜坡 的坡度为 ,点 到大楼的距离 为72米,求大楼的高度 .
(参考数据: , ,

某中学全校学生参加了"交通法规"知识竞赛,为了解全校学生竞赛成绩的情况,随机抽取了一部分学生的成绩,分成四组: ; ; ; ,并绘制出如图不完整的统计图.

(1)求被抽取的学生成绩在 组的有多少人?
(2)所抽取学生成绩的中位数落在哪个组内?
(3)若该学校有1500名学生,估计这次竞赛成绩在 组的学生有多少人?
如图,一次函数 的图象与反比例函数 的图象相交于 , 两点.
(1)求一次函数和反比例函数的表达式;
(2)直线 交 轴于点 ,点 是 轴上的点,若 的面积是4,求点 的坐标.

今年史上最长的寒假结束后,学生复学,某学校为了增强学生体质,鼓励学生在不聚集的情况下加强体育锻炼,决定让各班购买跳绳和毽子作为活动器材.已知购买2根跳绳和5个毽子共需32元;购买4根跳绳和3个毽子共需36元.
(1)求购买一根跳绳和一个毽子分别需要多少元?
(2)某班需要购买跳绳和毽子的总数量是54,且购买的总费用不能超过260元;若要求购买跳绳的数量多于20根,通过计算说明共有哪几种购买跳绳的方案.
如图,在 中, ,以 为直径的 与 相交于点 ,过点 作 的切线交 于点 .
(1)求证: ;
(2)若 的半径为5, ,求 的长.
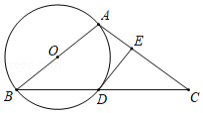
如图1,四边形 的对角线 , 相交于点 , , .
(1)过点 作 交 于点 ,求证: ;
(2)如图2,将 沿 翻折得到 .
①求证: ;
②若 ,求证: .

如图,抛物线 与 轴相交于 , 两点,与 轴相交于点 , , ,直线 是抛物线的对称轴,在直线 右侧的抛物线上有一动点 ,连接 , , , .
(1)求抛物线的函数表达式;
(2)若点 在 轴的下方,当 的面积是 时,求 的面积;
(3)在(2)的条件下,点 是 轴上一点,点 是抛物线上一动点,是否存在点 ,使得以点 , , , 为顶点,以 为一边的四边形是平行四边形,若存在,求出点 的坐标;若不存在,请说明理由.
