现实世界中,对称无处不在,在美术字中,有些汉字也具有对称性.下列汉字是轴对称图形的是
| A. |
|
B. |
|
C. |
|
D. |
|
据国家卫健委统计,截至6月2日,我国接种新冠疫苗已超过704000000剂次,把704000000这个数用科学记数法表示为
| A. |
|
B. |
|
C. |
|
D. |
|
如图所示,图中由7个完全相同小正方体组合而成的几何体,则这个几何体的左视图是
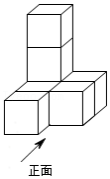
| A. |
|
B. |
|
C. |
|
D. |
|
若式子 在实数范围内有意义,则 的取值范围是
| A. |
|
B. |
且 |
C. |
且 |
D. |
|
定义一种新的运算:如果 .则有 ▲ ,那么 ▲2的值是
| A. |
|
B. |
5 |
C. |
|
D. |
|
下列命题是假命题的是
| A. |
任意一个三角形中,三角形两边的差小于第三边 |
| B. |
三角形的中位线平行于三角形的第三边,并且等于第三边的一半 |
| C. |
如果一个角的两边分别平行于另一个角的两边,那么这两个角一定相等 |
| D. |
一组对边平行且相等的四边形是平行四边形 |
下列运算正确的是
| A. |
|
B. |
|
C. |
|
D. |
|
一个多边形的内角和是外角和的4倍,则这个多边形是
| A. |
八边形 |
B. |
九边形 |
C. |
十边形 |
D. |
十二边形 |
近些年来,移动支付已成为人们的主要支付方式之一.某企业为了解员工某月 , 两种移动支付方式的使用情况,从企业2000名员工中随机抽取了200人,发现样本中 , 两种支付方式都不使用的有10人,样本中仅使用 种支付方式和仅使用 种支付方式的员工支付金额 (元 分布情况如表:
支付金额 (元 |
|
|
|
仅使用 |
36人 |
18人 |
6人 |
仅使用 |
20人 |
28人 |
2人 |
下面有四个推断:
①根据样本数据估计,企业2000名员工中,同时使用 , 两种支付方式的为800人;
②本次调查抽取的样本容量为200人;
③样本中仅使用 种支付方式的员工,该月支付金额的中位数一定不超过1000元;
④样本中仅使用 种支付方式的员工,该月支付金额的众数一定为1500元.
其中正确的是
| A. |
①③ |
B. |
③④ |
C. |
①② |
D. |
②④ |
根据市场需求,某药厂要加速生产一批药品,现在平均每天生产药品比原计划平均每天多生产500箱,现在生产6000箱药品所需时间与原计划生产4500箱药品所需时间相同,那么原计划平均每天生产多少箱药品?设原计划平均每天可生产 箱药品,则下面所列方程正确的是
| A. |
|
B. |
|
| C. |
|
D. |
|
已知在 中, , , ,点 为边 上的动点,点 为边 上的动点,则线段 的最小值是
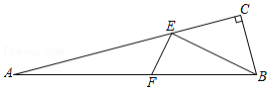
| A. |
|
B. |
|
C. |
|
D. |
|
如图所示,在矩形纸片 中, , ,点 、 分别是矩形的边 、 上的动点,将该纸片沿直线 折叠.使点 落在矩形边 上,对应点记为点 ,点 落在 处,连接 、 、 , 与 交于点 .则下列结论成立的是
① ;
②当点 与点 重合时, ;
③ 的面积 的取值范围是 ;
④当 时, .

| A. |
①③ |
B. |
③④ |
C. |
②③ |
D. |
②④ |
在单词 (数学)中任意选择一个字母恰好是字母“ ”的概率是 .
在实数范围内分解因式: .
一条弧所对的圆心角为 ,弧长等于半径为 的圆的周长的3倍,则这条弧的半径为 .
当 时,代数式 的值是 .
某学校计划为“建党百年,铭记党史”演讲比赛购买奖品.已知购买2个 种奖品和4个 种奖品共需100元;购买5个 种奖品和2个 种奖品共需130元.学校准备购买 , 两种奖品共20个,且 种奖品的数量不小于 种奖品数量的 ,则在购买方案中最少费用是 元.
已知 , 是一元二次方程 的两个根,则 .
边长为 的正六边形,它的外接圆与内切圆半径的比值是 .
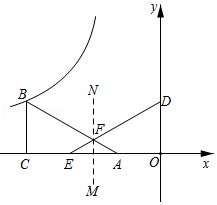
如图,在平面直角坐标系中, 为坐标原点, 垂直于 轴,以 为对称轴作 的轴对称图形,对称轴 与线段 相交于点 ,点 的对应点 恰好落在 的双曲线上,点 、 的对应点分别是点 、 .若点 为 的中点,且 ,则 的值为 .
在边长为4的正方形 中,连接对角线 、 ,点 是正方形边上或对角线上的一点,若 ,则 .
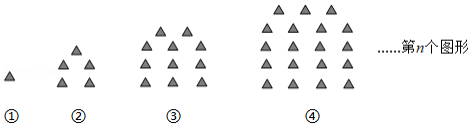
下面各图形是由大小相同的三角形摆放而成的,图①中有1个三角形,图②中有5个三角形,图③中有11个三角形,图④中有19个三角形 依此规律,则第 个图形中三角形个数是 .
(1)如图,已知 , 为边 上一点,请用尺规作图的方法在边 上求作一点 ,使 .(保留作图痕迹,不写作法)
(2)在图中,如果 , ,则 的周长是 .

如图所示,在网格中,每个小正方形的边长均为1个单位长度,把小正方形的顶点叫做格点, 为平面直角坐标系的原点,矩形 的4个顶点均在格点上,连接对角线 .
(1)在平面直角坐标系内,以原点 为位似中心,把 缩小,作出它的位似图形,并且使所作的位似图形与 的相似比等于 ;
(2)将 以 为旋转中心,逆时针旋转 ,得到△ ,作出△ ,并求,出线段 旋转过程中所形成扇形的周长.

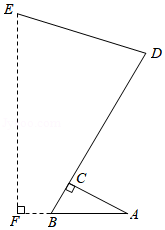
一种可折叠的医疗器械放置在水平地面上,这种医疗器械的侧面结构如图实线所示,底座为 ,点 、 、 在同一条直线上,测得 , , , ,其中一段支撑杆 ,另一段支撑杆 .求支撑杆上的点 到水平地面的距离 是多少?(用四舍五入法对结果取整数,参考数据: , , ,
小刚和小亮两人沿着直线跑道都从甲地出发,沿着同一方向到达乙地,甲乙两地之间的距离是720米,先到乙地的人原地休息.已知小刚先从甲地出发4秒后,小亮从甲地出发,两人均保持匀速前行第一次相遇后,保持原速跑一段时间,小刚突然加速,速度比原来增加了2米 秒,并保持这一速度跑到乙地(小刚加速过程忽略不计).小刚与小亮两人的距离 (米 与小亮出发时间 (秒 之间的函数图象,如图所示.根据所给信息解决以下问题.
(1) , ;
(2)求 和 所在直线的解析式;
(3)直接写出 为何值时,两人相距30米.

如图,在 中, ,以 为直径的 与 相交于点 , ,垂足为 .
(1)求证: 是 的切线;
(2)若弦 垂直于 ,垂足为 , , ,求 的半径;
(3)在(2)的条件下,当 时,求线段 的长.

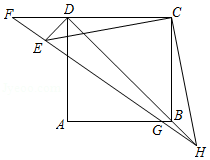
如图所示,四边形 为正方形,在 中, , , 的延长线与 的延长线交于点 ,点 、 、 在同一条直线上.
(1)求证: ;
(2)当 时,求 的值;
(3)当 , 时,求 的值.
如图,已知抛物线 与 轴交于点 ,点 (点 在点 的左边),与 轴交于点 ,点 为抛物线的顶点,连接 .直线 经过点 ,且与 轴交于点 .
(1)求抛物线的解析式;
(2)点 是抛物线上的一点,当 是以 为腰的等腰三角形时,求点 的坐标;
(3)点 为线段 上的一点,点 为线段 上的一点,连接 ,并延长 与线段 交于点 (点 在第一象限),当 且 时,求出点 的坐标.