下列四个实数中,最大的数是
| A. |
|
B. |
|
C. |
|
D. |
4 |
2021年5月11日,第七次全国人口普查结果发布,长沙市人口总数首次突破千万,约为10040000人,将数据10040000用科学记数法表示为
| A. |
|
B. |
|
C. |
|
D. |
|
下列几何图形中,是中心对称图形的是
| A. |
|
B. |
|
C. |
|
D. |
|
下列计算正确的是
| A. |
|
B. |
|
C. |
|
D. |
|
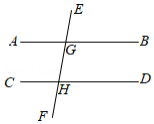
如图, , 分别与 , 交于点 , , ,则 的度数为
| A. |
|
B. |
|
C. |
|
D. |
|
如图,点 , , 在 上, ,则 的度数为

| A. |
|
B. |
|
C. |
|
D. |
|
下列函数图象中,表示直线 的是
| A. |
|
B. |
|
| C. |
|
D. |
|
"杂交水稻之父"袁隆平培育的超级杂交稻在全世界推广种植.某种植户为了考察所种植的杂交水稻苗的长势,从稻田中随机抽取9株水稻苗,测得苗高(单位: 分别是:22,23,24,23,24,25,26,23,25.则这组数据的众数和中位数分别是
| A. |
24,25 |
B. |
23,23 |
C. |
23,24 |
D. |
24,24 |
有一枚质地均匀的正方体骰子,六个面上分别刻有1到6的点数.将它投掷两次,则两次掷得骰子朝上一面的点数之和为5的概率是
| A. |
|
B. |
|
C. |
|
D. |
|
在一次数学活动课上,某数学老师将 共十个整数依次写在十张不透明的卡片上(每张卡片上只写一个数字,每一个数字只写在一张卡片上,而且把写有数字的那一面朝下).他先像洗扑克牌一样打乱这些卡片的顺序,然后把甲,乙,丙,丁,戊五位同学叫到讲台上,随机地发给每位同学两张卡片,并要求他们把自己手里拿的两张卡片上的数字之和写在黑板上,写出的结果依次是:甲:11;乙:4;丙:16;丁:7;戊:17.根据以上信息,下列判断正确的是
| A. |
戊同学手里拿的两张卡片上的数字是8和9 |
| B. |
丙同学手里拿的两张卡片上的数字是9和7 |
| C. |
丁同学手里拿的两张卡片上的数字是3和4 |
| D. |
甲同学手里拿的两张卡片上的数字是2和9 |
分解因式: .
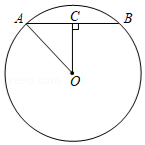
如图,在 中,弦 的长为4,圆心到弦 的距离为2,则 的度数为 .
如图,菱形 的对角线 , 相交于点 ,点 是边 的中点,若 ,则 的长为 .

若关于 的方程 的一个根为3,则 的值为 .
如图,在 中, , 平分 交 于点 , ,垂足为 ,若 , ,则 的长为 .

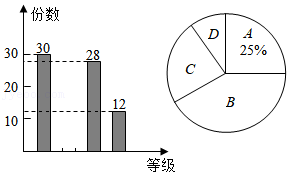
某学校组织了主题为"保护湘江,爱护家园"的手抄报作品征集活动.先从中随机抽取了部分作品,按 , , , 四个等级进行评价,然后根据统计结果绘制了如图两幅不完整的统计图.那么,此次抽取的作品中,等级为 等的作品份数为 .
计算: .
先化简,再求值: ,其中 .
人教版初中数学教科书八年级上册第 页告诉我们作一个三角形与已知三角形全等的方法:
已知: . 求作:△ ,使得△ . 作法:如图. (1)画 ; (2)分别以点 , 为圆心,线段 , 长为半径画弧,两弧相交于点 ; (3)连接线段
,
,则△
即为所求作的三角形. |
请你根据以上材料完成下列问题:
(1)完成下面证明过程(将正确答案填在相应的空上)
证明:由作图可知,在△ 和 中,
△ .
(2)这种作一个三角形与已知三角形全等的方法的依据是 .(填序号)
①
②
③
④
“网红”长沙入选2021年“五一”假期热门旅游城市.本市某景点为吸引游客,设置了一种游戏,其规则如下:凡参与游戏的游客从一个装有12个红球和若干个白球(每个球除颜色外,其他都相同)的不透明纸箱中,随机摸出一个球,摸到红球就可免费得到一个景点吉祥物.据统计参与这种游戏的游客共有60000人,景点一共为参与该游戏的游客免费发放了景点吉祥物15000个.
(1)求参与该游戏可免费得到景点吉祥物的频率;
(2)请你估计纸箱中白球的数量接近多少?
如图, 的对角线 , 相交于点 , 是等边三角形, .
(1)求证: 是矩形;
(2)求 的长.
为庆祝伟大的中国共产党成立100周年,发扬红色传统,传承红色精神,某学校举行了主题为“学史明理,学史增信,学史崇德,学史力行”的党史知识竞赛,一共有25道题,满分100分,每一题答对得4分,答错扣1分,不答得0分.
(1)若某参赛同学只有一道题没有作答,最后他的总得分为86分,则该参赛同学一共答对了多少道题?
(2)若规定参赛者每道题都必须作答且总得分大于或等于90分才可以被评为“学党史小达人”,则参赛者至少需答对多少道题才能被评为“学党史小达人”?
如图,在 中, ,垂足为 , ,延长 至 ,使得 ,连接 .
(1)求证: ;
(2)若 , ,求 的周长和面积.
我们不妨约定:在平面直角坐标系中,若某函数图象上至少存在不同的两点关于 轴对称,则把该函数称之为“ 函数”,其图象上关于 轴对称的不同两点叫做一对“ 点”.根据该约定,完成下列各题.
(1)若点 与点 是关于 的“ 函数” 的图象上的一对“ 点”,则 , , (将正确答案填在相应的横线上);
(2)关于 的函数 , 是常数)是“ 函数”吗?如果是,指出它有多少对“ 点”如果不是,请说明理由;
(3)若关于 的“ 函数” ,且 , , 是常数)经过坐标原点 ,且与直线 , ,且 , 是常数)交于 , , , 两点,当 , 满足 时,直线 是否总经过某一定点?若经过某一定点,求出该定点的坐标;否则,请说明理由.
如图,点 为以 为直径的半圆的圆心,点 , 在直径 上,点 , 在 上,四边形 为正方形,点 在 上运动(点 与点 , 不重合),连接 并延长交 的延长线于点 ,连接 交 于点 ,连接 .
(1)求 的值;
(2)求 的值;
(3)令 , ,直径 , 是常数),求 关于 的函数解析式,并指明自变量 的取值范围.