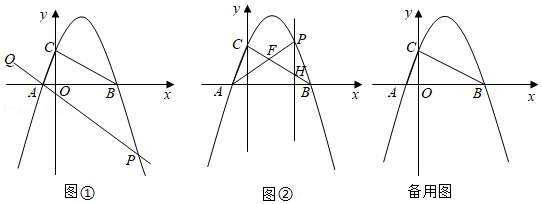
的相反数为
| A. |
|
B. |
|
C. |
|
D. |
3 |
对称美是美的一种重要形式,它能给与人们一种圆满、协调和平的美感,下列图形属于中心对称图形的是
| A. |
|
B. |
|
C. |
|
D. |
|
下列运算正确的是
| A. |
|
B. |
|
C. |
|
D. |
|
已知一组数据:4,3,4,5,6,则这组数据的中位数是
| A. |
3 |
B. |
3.5 |
C. |
4 |
D. |
4.5 |
如图,在 中, , , 平分 交 于点 , ,交 于点 ,则 的度数是

| A. |
|
B. |
|
C. |
|
D. |
|
已知双曲线 过点 、 、 ,则下列结论正确的是
| A. |
|
B. |
|
C. |
|
D. |
|
如图,折叠矩形纸片 ,使点 落在点 处,折痕为 ,已知 , ,则 的长是

| A. |
|
B. |
|
C. |
|
D. |
|
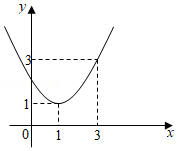
已知二次函数 的图象如图所示,有下列结论:① ;② ;③ ;④不等式 的解集为 ,正确的结论个数是
| A. |
1 |
B. |
2 |
C. |
3 |
D. |
4 |
若代数式 有意义,则 的取值范围是 .
2021年4月,白鹤滩水电站正式开始蓄水,首批机组投产发电开始了全国冲刺,该电站建成后,将仅次于三峡水电站成为我国第二大水电站,每年可减少二氧化碳排放51600000吨,减碳成效显著,对促进我市实现碳中和目标具有重要作用,51600000用科学记数法表示为 .
分解因式: .
方程 的解是 .
已知圆锥的底面圆半径为4,侧面展开图扇形的圆心角为 ,则它的侧面展开图面积为 .
若关于 的一元二次方程 的一个根是3,则 .
《九章算术》中一道"引葭赴岸"问题:"今有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深,葭长各几何?"题意是:有一个池塘,其地面是边长为10尺的正方形,一棵芦苇 生长在它的中央,高出水面部分 为1尺,如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部 恰好碰到岸边的 处(如图),水深和芦苇长各多少尺?则该问题的水深是 尺.

如图,在 中, , ,点 、 在 上,边 、 分别交 于 、 两点,点 是 的中点,则 .

如图,点 、 在反比例函数 的图象上,延长 交 轴于 点,若 的面积是12,且点 是 的中点,则 .

如图,在 中, , ,点 、 分别在 、 上, , , 交 于点 ,则 面积的最大值是 .

计算: .
解不等式组 ,并写出满足不等式组的所有整数解.
某机构为了解宿迁市人口年龄结构情况,对宿迁市的人口数据进行随机抽样分析,绘制了尚不完整的统计图表:
人口年龄结构统计表
类别 |
|
|
|
|
年龄 岁) |
|
|
|
|
人数(万人) |
4.7 |
11.6 |
|
2.7 |
根据以上信息解答下列问题:
(1)本次抽样调查,共调查了 万人;
(2)请计算统计表中 的值以及扇形统计图中“ ”对应的圆心角度数;
(3)宿迁市现有人口约500万人,请根据此次抽查结果,试估计宿迁市现有60岁及以上的人口数量.

在① ;② ;③ 这三个条件中任选一个补充在下面横线上,并完成证明过程.
已知,如图,四边形 是平行四边形,对角线 、 相交于点 ,点 、 在 上, (填写序号).
求证: .

即将举行的2022年杭州亚运会吉祥物"宸宸"、"琮琮"、"莲莲",将三张正面分别印有以上3个吉祥物图案的卡片(卡片的形状、大小、质地都相同)背面朝上、洗匀.

(1)若从中任意抽取1张,抽得卡片上的图案恰好为"莲莲"的概率是 .
(2)若先从中任意抽取1张,记录后放回,洗匀,再从中任意抽取1张,求两次抽取的卡片图案相同的概率.(请用树状图或列表的方法求解)
一架无人机沿水平直线飞行进行测绘工作,在点 处测得正前方水平地面上某建筑物 的顶端 的俯角为 ,面向 方向继续飞行5米,测得该建筑物底端 的俯角为 ,已知建筑物 的高为3米,求无人机飞行的高度(结果精确到1米,参考数据: , .

如图,在 中, ,以点 为圆心, 为半径的圆交 于点 ,点 在边 上,且 .
(1)判断直线 与 的位置关系,并说明理由;
(2)已知 , ,求 的半径.

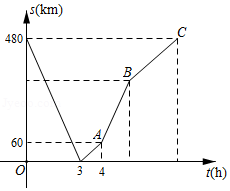
一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶,两车在途中相遇时,快车恰巧出现故障,慢车继续驶往甲地,快车维修好后按原速继续行驶乙地,两车到达各地终点后停止,两车之间的距离 与慢车行驶的时间 之间的关系如图:
(1)快车的速度为 , 点的坐标为 .
(2)慢车出发多少小时后,两车相距 .
已知正方形 与正方形 ,正方形 绕点 旋转一周.
(1)如图①,连接 、 ,求 的值;
(2)当正方形 旋转至图②位置时,连接 、 ,分别取 、 的中点 、 ,连接 、试探究: 与 的关系,并说明理由;
(3)连接 、 ,分别取 、 的中点 、 ,连接 , ,请直接写出线段 扫过的面积.

如图,抛物线 与 轴交于 , ,与 轴交于点 .连接 , ,点 在抛物线上运动.
(1)求抛物线的表达式;
(2)如图①,若点 在第四象限,点 在 的延长线上,当 时,求点 的坐标;
(3)如图②,若点 在第一象限,直线 交 于点 ,过点 作 轴的垂线交 于点 ,当 为等腰三角形时,求线段 的长.