下列各数中,是负数的是
| A. |
|
B. |
|
C. |
|
D. |
|
如图所示的几何体,其上半部有一个圆孔,则该几何体的俯视图是

| A. |
|
B. |
|
| C. |
|
D. |
|
已知一个水分子的直径约为 米,某花粉的直径约为 米,用科学记数法表示一个水分子的直径是这种花粉直径的
| A. |
倍 |
B. |
倍 |
C. |
倍 |
D. |
倍 |
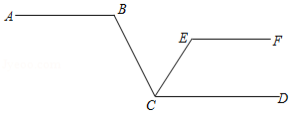
如图, ,若 , ,则 的度数为
| A. |
|
B. |
|
C. |
|
D. |
|
为了保护环境加强环保教育,某中学组织学生参加义务收集废旧电池的活动,下面是随机抽取40名学生对收集废旧电池的数量进行的统计:
废旧电池数 节 |
4 |
5 |
6 |
7 |
8 |
人数 人 |
9 |
11 |
11 |
5 |
4 |
请根据学生收集到的废旧电池数,判断下列说法正确的是
| A. |
样本为40名学生 |
B. |
众数是11节 |
| C. |
中位数是6节 |
D. |
平均数是5.6节 |
下列运算正确的是
| A. |
|
B. |
|
| C. |
|
D. |
|
关于 的方程 的一个解是 ,则 值为
| A. |
2或4 |
B. |
0或4 |
C. |
或0 |
D. |
或2 |
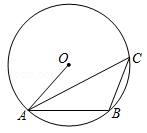
如图, , , 是半径为1的 上的三个点,若 , ,则 的度数为
| A. |
|
B. |
|
C. |
|
D. |
|
若 ,则关于 的方程 解的取值范围为
| A. |
|
B. |
|
C. |
|
D. |
|
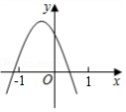
已知二次函数 的图象如图所示,则一次函数 的图象和反比例函数 的图象在同一坐标系中大致为
| A. |
|
B. |
|
| C. |
|
D. |
|
如图,在直角坐标系中,点 , 的坐标为 , ,将 绕点 按顺时针旋转得到△ ,若 ,则点 的坐标为
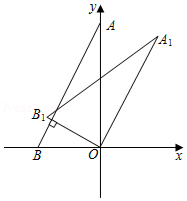
| A. |
, |
B. |
, |
C. |
, |
D. |
, |
如图,四边形 中,已知 , 与 之间的距离为4, , , ,点 , 同时由 点出发,分别沿边 ,折线 向终点 方向移动,在移动过程中始终保持 ,已知点 的移动速度为每秒1个单位长度,设点 的移动时间为 秒, 的面积为 ,则能反映 与 之间函数关系的图象是
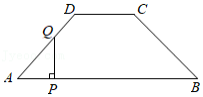
| A. |
|
B. |
|
| C. |
|
D. |
|
计算: .
有四张大小和背面完全相同的不透明卡片,正面分别印有等边三角形、平行四边形、菱形和圆,将这四张卡片背面朝上洗匀,从中随机抽取两张卡片,所抽取的卡片正面上的图形都既是轴对称图形,又是中心对称图形的概率是 .
如图,在 中, , ,垂足分别为点 和点 , 与 交于点 ,连接 并延长交 于点 ,若 , , ,则 值为 .

用一块弧长 的扇形铁片,做一个高为 的圆锥形工件侧面(接缝忽略不计),那么这个扇形铁片的面积为 .
如图,在直角坐标系中,矩形 的顶点 在坐标原点,顶点 , 分别在 轴, 轴上, , 两点坐标分别为 , ,线段 在边 上移动,保持 ,当四边形 的周长最小时,点 的坐标为 .

先化简,再求值: ,其中 .
为扎实推进“五育并举”工作,某校根据课外活动时间,开设了书法、健美操、乒乓球和朗诵四个社团活动,每个学生选择一项活动参加,为了了解活动开展情况,学校随机抽取了部分学生进行调查,将调查结果绘制成条形统计图和扇形统计图:

请根据以上的信息,回答下列问题:
(1)抽取的学生有 人, , ;
(2)补全条形统计图;
(3)若该校有学生3200人,估计参加书法社团活动的学生人数.
为迎接建党一百周年,我市计划用两种花卉对某广场进行美化.已知用600元购买 种花卉与用900元购买 种花卉的数量相等,且 种花卉每盆比 种花卉多0.5元.
(1) , 两种花卉每盆各多少元?
(2)计划购买 , 两种花卉共6000盆,其中 种花卉的数量不超过 种花卉数量的 ,求购买 种花卉多少盆时,购买这批花卉总费用最低,最低费用是多少元?
如图,在四边形 中, 与 相交于点 ,且 ,点 在 上,满足 .
(1)求证:四边形 是平行四边形;
(2)若 , , ,求四边形 的面积.

时代中学组织学生进行红色研学活动.学生到达爱国主义教育基地后,先从基地门口 处向正南方向走300米到达革命纪念碑 处,再从 处向正东方向走到党史纪念馆 处,然后从 处向北偏西 方向走200米到达人民英雄雕塑 处,最后从 处回到 处.已知人民英雄雕塑在基地门口的南偏东 方向,求革命纪念碑与党史纪念馆之间的距离(精确到1米).(参考数据: , , , , ,
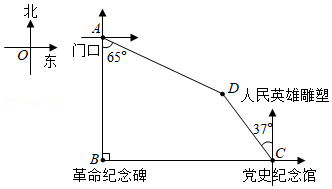
如图,过 点的直线 与 轴, 轴分别交于点 , 两点,且 ,过点 作 轴,垂足为点 ,交反比例函数 的图象于点 ,连接 , 的面积为6.
(1)求 值和点 的坐标;
(2)如图,连接 , ,点 在直线 上,且位于第二象限内,若 的面积是 面积的2倍,求点 的坐标.

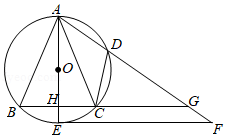
如图,在 中, , 是 的外接圆, 是直径,交 于点 ,点 在 上,连接 , 过点 作 交 的延长线于点 ,延长 交 于点 .
(1)求证: 是 的切线;
(2)若 , ,求 和 的长.
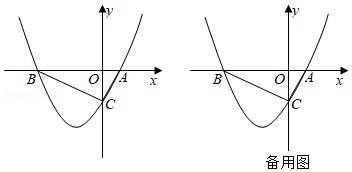
如图,抛物线 与 轴交于点 , ,与 轴交于点 ,已知 , 两点坐标分别是 , ,连接 , .
(1)求抛物线的表达式和 所在直线的表达式;
(2)将 沿 所在直线折叠,得到 ,点 的对应点 是否落在抛物线的对称轴上,若点 在对称轴上,请求出点 的坐标;若点 不在对称轴上,请说明理由;
(3)若点 是抛物线位于第三象限图象上的一动点,连接 交 于点 ,连接 , 的面积记为 , 的面积记为 ,求 的值最大时点 的坐标.