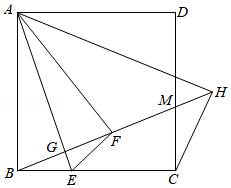
的相反数是
| A. |
|
B. |
|
C. |
2 |
D. |
|
2021年5月15日,天问一号探测器成功着陆火星,中国成为全世界第二个实现火星着陆的国家.据测算,地球到火星的最近距离约为 ,将数据55000000用科学记数法表示为
| A. |
|
B. |
|
C. |
|
D. |
|
计算 的结果是
| A. |
|
B. |
|
C. |
|
D. |
|
如图所示的几何体的主视图是

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在 中, , 平分 ,则 的度数为

| A. |
|
B. |
|
C. |
|
D. |
|
方程 的根是
| A. |
, |
B. |
, |
C. |
, |
D. |
, |
不等式 的解集在数轴上表示正确的是
| A. |
|
B. |
|
| C. |
|
D. |
|
计算 的结果是
| A. |
|
B. |
|
C. |
|
D. |
|
如图,每一小格的长度为1,点 , 都在格点上,若 ,则 的长为

| A. |
|
B. |
|
C. |
|
D. |
|
现有4盒同一品牌的牛奶,其中2盒已过期,随机抽取2盒,至少有一盒过期的概率是
| A. |
|
B. |
|
C. |
|
D. |
|
如图, 、 分别与 相切于 、 , , 为 上一点,则 的度数为

| A. |
|
B. |
|
C. |
|
D. |
|
某工厂生产 、 两种型号的扫地机器人. 型机器人比 型机器人每小时的清扫面积多 ;清扫 所用的时间 型机器人比 型机器人多用40分钟.两种型号扫地机器人每小时分别清扫多少面积?若设 型扫地机器人每小时清扫 ,根据题意可列方程为
| A. |
|
B. |
|
| C. |
|
D. |
|
已知 ,下列结论:① ;② ;③若 ,则 ;④若 ,则 ,其中正确的个数是
| A. |
1 |
B. |
2 |
C. |
3 |
D. |
4 |
实验证实,放射性物质在放出射线后,质量将减少,减少的速度开始较快,后来较慢,实际上,物质所剩的质量与时间成某种函数关系.
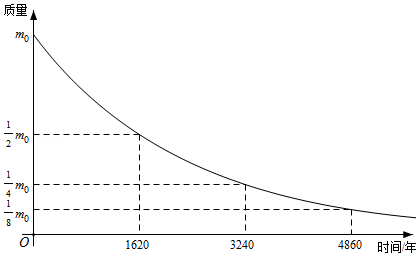
如图为表示镭的放射规律的函数图象,据此可计算 镭缩减为 所用的时间大约是
| A. |
4860年 |
B. |
6480年 |
C. |
8100年 |
D. |
9720年 |
分解因式: .
比较大小: 5(选填“ ”、“ ”、“ ” .
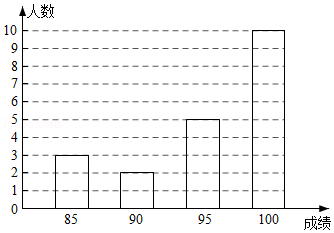
某学校八年级(2)班有20名学生参加学校举行的"学党史、看红书"知识竞赛,成绩统计如图.这个班参赛学生的平均成绩是 .
在平面直角坐标系中,平行四边形 的对称中心是坐标原点,顶点 、 的坐标分别是 、 ,将平行四边形 沿 轴向右平移3个单位长度,则顶点 的对应点 的坐标是 .
数学知识在生产和生活中被广泛应用,下列实例所应用的最主要的几何知识,说法正确的是 (只填写序号).
①射击时,瞄准具的缺口、准星和射击目标在同一直线上,应用了"两点确定一条直线";
②车轮做成圆形,应用了"圆是中心对称图形";
③学校门口的伸缩门由菱形而不是其他四边形组成,应用了"菱形的对角线互相垂直平分";
④地板砖可以做成矩形,应用了"矩形对边相等".

计算 .
实施乡村振兴计划以来,我市农村经济发展进入了快车道,为了解梁家岭村今年一季度经济发展状况,小玉同学的课题研究小组从该村300户家庭中随机抽取了20户,收集到他们一季度家庭人均收入的数据如下(单位:万元)
0.69 0.73 0.74 0.80 0.81 0.98 0.93 0.81 0.89 0.69
0.74 0.99 0.98 0.78 0.80 0.89 0.83 0.89 0.94 0.89
研究小组的同学对以上数据进行了整理分析,得到下表:
分组 |
频数 |
|
2 |
|
3 |
|
1 |
|
|
|
4 |
|
2 |
|
|
统计量 |
平均数 |
中位数 |
众数 |
数值 |
0.84 |
|
|
(1)表格中: , , , ;
(2)试估计今年一季度梁家岭村家庭人均收入不低于0.8万元的户数;
(3)该村梁飞家今年一季度人均收入为0.83万元,能否超过村里一半以上的家庭?请说明理由.
如图,在某小区内拐角处的一段道路上,有一儿童在 处玩耍,一辆汽车从被楼房遮挡的拐角另一侧的 处驶来,已知 , , , ,汽车从 处前行多少米才能发现 处的儿童(结果保留整数)?
(参考数据: , , ; , ,

已知函数
(1)画出函数图象;
列表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
描点,连线得到函数图象:
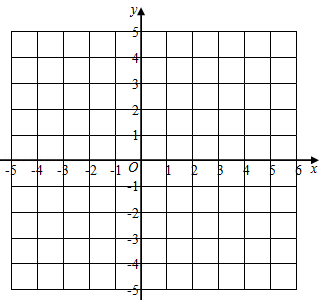
(2)该函数是否有最大或最小值?若有,求出其值,若没有,简述理由;
(3)设 , , , 是函数图象上的点,若 ,证明: .
如图,已知在 中, , 与 相交于点 .
求证:(1) ;
(2)四边形 为菱形.

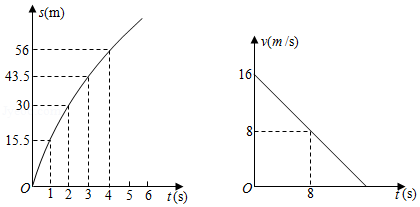
公路上正在行驶的甲车,发现前方 处沿同一方向行驶的乙车后,开始减速,减速后甲车行驶的路程 (单位: 、速度 (单位: 与时间 (单位: 的关系分别可以用二次函数和一次函数表示,其图象如图所示.
(1)当甲车减速至 时,它行驶的路程是多少?
(2)若乙车以 的速度匀速行驶,两车何时相距最近,最近距离是多少?
如图,已知正方形 ,点 是 边上一点,将 沿直线 折叠,点 落在 处,连接 并延长,与 的平分线相交于点 ,与 , 分别相交于点 , ,连接 .
(1)求证: ;
(2)若 , ,求点 到直线 的距离;
(3)当点 在 边上(端点除外)运动时, 的大小是否变化?为什么?