已知集合 , 则 )
| A. |
|
| B. |
|
| C. |
|
| D. |
|
若 满足 ,则 的最大值为( )
| A. |
0 |
B. |
3 |
C. |
4 |
D. |
5 |
执行如图所示的程序框图, 若输入的 值为 1, 则输出的 值为( )

| A. |
1 |
B. |
2 |
C. |
3 |
D. |
4 |
设 是向量, 则 是 的( )
| A. |
充分而不必要条件 |
| B. |
必要而不充分条件 |
| C. |
充分必要条件 |
| D. |
既不充分也不必要条件 |
已知 , 且 , 则( )
| A. |
|
B. |
|
C. |
|
D. |
|
某三棱锥的三视图如图所示, 则该三棱雉的体积为( )
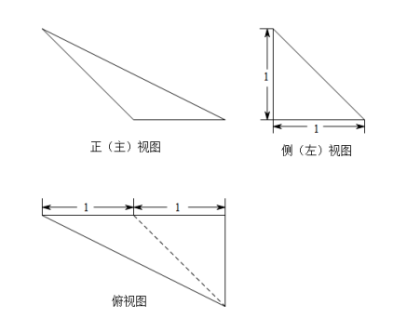
| A. |
|
B. |
|
C. |
|
D. |
1 |
将函数 图象上的点 向左平移 个单位长度得到点 , 若 位于函数 的图象上, 则( )
| A. |
的最小值为 |
B. |
的最小值为 |
| C. |
的最小值为 |
D. |
的最小值为 |
袋中装有偶数个球,其中红球、黑球各占一半.甲、乙、丙是三个空盒.每次从袋中 任意取出两个球, 将其中一个球放入甲盒, 如果这个球是红球, 就将另一个球放入乙盒, 否则就放入丙盒.重复上述过程, 直到袋中所有球都被放入盒中, 则( )
| A. |
乙盒中黑球不多于丙盒中黑球; |
| B. |
乙盒中红球与丙盒中黑球一样多; |
| C. |
乙盒中红球不多于丙盒中红球; |
| D. |
乙盒中黑球与丙盒中红球一样多; |
设 , 若复数 在复平面内对应的点位于实轴上, 则
。
在 的展开式中, 的系数为_ (用数字作答)
在极坐标系中, 直线 与圆 交于 两点,则 。
已知 为等差数列, 为其前 项和, 若 , 则 。
双曲线 的渐近线为正方形 的边 所在的直线, 点 为该双曲线的焦点, 若正方形 的边长为 2 , 则 .
设函数 .
(1)若 , 则 的最大值为_ 。
(2)若 无最大值, 则实数 的取值范围是_ 。
在 中, .
(1) 求 的大小;
(2) 求 的最大值.
A、B、C三个班共有 100 名学生, 为调查他们的体育锻炼情况,通过分层抽样获得了部分学生 一周的锻炼时间, 数据如下表(单位:小时);
A 班 |
|
7 |
|
|||||
B 班 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
C 班 |
3 |
|
6 |
|
9 |
|
12 |
|
(1)试估计 C 班的学生人数;
(2) 从 A 班和 班抽出的学生中, 各随机选取一人, 班选出的人记为甲, 班选出的人记 为乙, 假设所有学生的锻炼时间相对独立, 求该周甲的锻炼时间比乙的钗炼时间长的概率;
(3) 再从 A、B、C三个班中各随机抽取一名学生, 他们该周的锻炼时间分别是 7, 9, 8.25 (单位:小时), 这3个新数据与表格中的数据构成的新样本的平均数记 , 表格中数据的平均数记为 , 试判断 和 的大小, (结论不要求证明)
如图, 在四棱锥 中, 平面 平面 , .

(1) 求证: 平面 ;
(2) 求直线 与平面 所成角的正弦值;
(3) 在棱 上是否存在点 , 使得 平面 ? 若存在, 求 的值; 若不存在, 说明理由.
设函数 , 曲线 在点 处的切线方程为 ,
(1)求 的值;
(2)求 的单调区间;
已知椭圆
的离心率为
的面积为 1 .
(1) 求椭圆 C 的方程;
(2) 设 的椭圆 上一点, 直线 与 轴交于点 , 直线 与 轴交于点 .
求证: 为定值.
, 则称 是数列 的一个 " 时刻" 记 是数列 的所有 " 时刻" 组成的集合.
(1)对数列 A: , 写出 的所有元素;
(2)证明:若数列 中存在 使得 , 则 ;
(3)证明:若数列 满足 则G(A)的元素个数小于 ;