已知集合 , ,则 ( )
| A. |
|
B. |
|
C. |
|
D. |
|
( )
| A. |
|
B. |
|
C. |
|
D. |
|
中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是( )
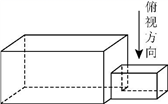
| A. |
|
B. |
|
C. |
|
D. |
|
若 ,则 ( )
| A. |
|
B. |
|
C. |
|
D. |
|
若某群体中的成员只用现金支付的概率为0.45,既用现金支付也用非现金支付的概率为0.15,则不用现金支付的概率为( )
| A. |
0.3 |
B. |
0.4 |
C. |
0.6 |
D. |
0.7 |
函数 的最小正周期为( )
| A. |
|
B. |
|
C. |
|
D. |
|
下列函数中,其图像与函数 的图像关于直线 对称的是( )
| A. |
|
B. |
|
C. |
|
D. |
|
直线 分别与 轴, 轴交于 , 两点,点 在圆 上,则 面积的取值范围是( )
| A. |
|
B. |
|
C. |
|
D. |
|
函数 的图像大致为( )
| A. |
|
B. |
|
| C. |
|
D. |
|
已知双曲线 的离心率为 ,则点 到 的渐近线的距离为( )
| A. |
|
B. |
|
C. |
|
D. |
|
的内角 的对边分别为 , , ,若 的面积为 ,则 ( )
| A. |
|
B. |
|
C. |
|
D. |
|
设 是同一个半径为4的球的球面上四点, 为等边三角形且其面积为 ,则三棱锥 体积的最大值为( )
A. B. C. D.
已知向量 , , .若 ,则 ________.
某公司有大量客户,且不同龄段客户对其服务的评价有较大差异.为了解客户的评价,该公司准备进行抽样调查,可供选择的抽样方法有简单随机抽样、分层抽样和系统抽样,则最合适的抽样方法是________.
若变量 满足约束条件 则 的最大值是________.
已知函数 , ,则 ________.
等比数列 中, .
(1)求 的通项公式;
(2)记 为 的前 项和.若 ,求 .
某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了如下茎叶图:
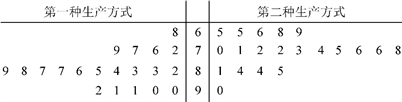
(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;
(2)求40名工人完成生产任务所需时间的中位数 ,并将完成生产任务所需时间超过 和不超过 的工人数填入下面的列联表:
超过 |
不超过 |
|
第一种生产方式 |
||
第二种生产方式 |
(3)根据(2)中的列联表,能否有99%的把握认为两种生产方式的效率有差异?
附: ,
|
|
|
|
|
|
|
|
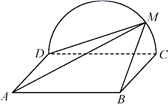
如图,矩形 所在平面与半圆弧 所在平面垂直, 是 上异于 , 的点.
(1)证明:平面 平面 ;
(2)在线段 上是否存在点 ,使得 平面 ?说明理由.
已知斜率为 的直线 与椭圆 交于 , 两点.线段 的中点为 .
(1)证明: ;
(2)设 为 的右焦点, 为 上一点,且 .证明: .
已知函数 .
(1)求曲线 在点
处的切线方程;
在点
处的切线方程;
(2)证明:当 时, .
在平面直角坐标系 中, 的参数方程为 ( 为参数),过点 且倾斜角为 的直线 与 交于 两点.
(1)求 的取值范围;
(2)求 中点 的轨迹的参数方程.
设函数 .
(1)画出 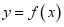 的图像;
的图像;
(2)当 , ,求 的最小值.