已知 为等差数列, ,则 等于( )
| A. |
|
B. |
|
C. |
|
D. |
|
设 是实数,则" "是" "的( )
| A. | 充分而不必要条件 |
B. | 必要而不充分条件 |
| C. | 充要条件 |
D. | 既不充分也不必要条件 |
曲线 C: ( 为参数)的普通方程为( )
| A. |
|
B. |
|
| C. |
|
D. |
|
若点 分有向线段 所成的比为 ,则点 分有向线段 所成的比是( )
| A. |
|
B. |
|
C. |
|
D. |
|
某交高三年级有男生500人,女生400人,为了解该年级学生的健康情况,从男生中任意抽取25人,从女生中任意抽取20人进行调查.这种抽样方法是( )
| A. |
简单随机抽样法 |
B. |
抽签法 |
C. |
随机数表法 |
D. |
分层抽样法 |
函数 的反函数是( )
| A. |
|
B. | ( ) |
| C. | ( ) |
D. | ( ) |
函数 的最大值为( )
| A. |
|
B. |
|
C. |
|
D. |
|
若双曲线 的左焦点在抛物线 的准线上,则 的值为( )
| A. |
|
B. |
|
C. |
|
D. |
|
从编号为1,2,…,10的10个大小相同的球中任取4个,则所取4个球的最大号码是6的概率为( )
| A. |
|
B. |
|
C. |
|
D. |
|
若 的展开式中前三项的系数成等差数,则展开式中 项的系数为( )
| A. |
|
B. |
|
C. |
|
D. |
|
如图,模块①-⑤均由4个棱长为1的小正方体构成,模块⑥由15个棱长为1的小正方体构成.现从模块①-⑤中选出三个放到模块⑥上,使得模块⑥成为一个棱长为3的大正方体.则下列选择方案中,能够完成任务的为( )

| A. |
模块①,②,⑤ |
B. |
模块①,③,⑤ |
| C. |
模块②,④,⑥ |
D. |
模块③,④,⑤ |
函数 的值域是( )
| A. |
|
B. |
|
C. |
|
D. |
|
已知集合 ,则 .
若 则 = .
已知圆 : 上任意一点关于直线 的对称点都在圆 上,则 .
某人有3种颜色的灯泡(每种颜色的灯泡足够多),要在如图所示的6个点 、 、 、 、 、 上各安装一个灯泡,要求同一条线段两端的灯泡不同色,则不同的安装方法共有 种(用数字作答).

设 的内角 , , 的对边分别为 , , .已知 ,求:
(Ⅰ) 的大小;
(Ⅱ) 的值.
在每道单项选择题给出的4个备选答案中,只有一个是正确的.若对4道选择题中的每一道都任意选定一个答案,求这4道题中:
(Ⅰ)恰有两道题答对的概率;
(Ⅱ)至少答对一道题的概率.
设函数 若曲线 的斜率最小的切线与直线 平行,求:
(Ⅰ) 的值;
(Ⅱ)函数 的单调区间.
如图,  为平面,
,
,
在棱
上的射影分别为
,
,
,
.若二面角
的大小为
,求:
为平面,
,
,
在棱
上的射影分别为
,
,
,
.若二面角
的大小为
,求:

(Ⅰ)点 到平面 的距离;
(Ⅱ)异面直线 与 所成的角(用反三角函数表示).
如图, 和 是平面上的两点,动点 满足:
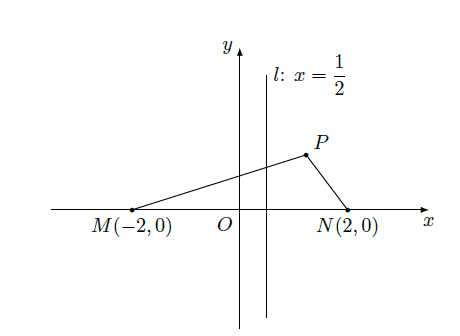
(Ⅰ)求点 的轨迹方程;
(Ⅱ)设 为点 到直线 : 的距离,若 ,求 的值.
设各项均为正数的数列 满足 .
(Ⅰ)若 求 , ,并猜想 的值(不需证明);
(Ⅱ)若 对 恒成立,求 的值.