若集合 , ,则 ( )
| A. |
|
B. |
|
C. |
|
D. |
|
若复数 在复平面内对应的点在第二象限,则实数a的取值范围是( )
| A. |
|
B. |
|
C. |
|
D. |
|
执行如图所示的程序框图,输出的S值为( )
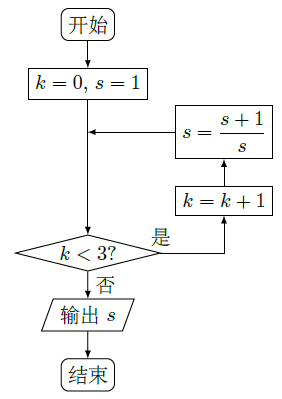
| A. | 2 |
B. |
|
C. |
|
D. |
|
若 满足 ,则 的最大值为( )
| A. |
1 |
B. |
3 |
C. |
5 |
D. |
9 |
已知函数 , 则 ( )
| A. |
是奇函数,且在R上是增函数 |
B. |
是偶函数,且在R上是增函数 |
| C. |
是奇函数,且在R上是减函数 |
D. |
是偶函数,且在R上是减函数 |
设 , 为非零向量,则"存在负数 ,使得 "是 " "的( )
| A. |
充分而不必要条件 |
B. |
必要而不充分条件 |
C. |
充分必要条件 |
D. |
既不充分也不必要条件 |
某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为( )

| A. |
|
B. |
|
C. |
|
D. | 2 |
根据有关资料,围棋状态空间复杂度的上限M约为 , 而可观测宇宙中普通物质的原子总数N约为 , 则下列各数中与 最接近的是( )
(参考数据: )
| A. |
|
B. |
|
C. |
|
D. |
|
若双曲线 的离心率为 ,则实数 ________.
若等差数列 和等比数列 满足 , ,则 =________.
在极坐标系中,点A在圆 上,点P的坐标为 ,则 的最小值为________.
在平面直角坐标系 中,角 与角 均以 为始边,它们的终边关于 轴对称,若 ,则 ________.
能够说明“设a,b,c是任意实数.若 ,则 ”是假命题的一组整数a,b,c的值依次为________.
三名工人加工同一种零件,他们在一天中的工作情况如图所示,其中 的横、纵坐标分别为第 名工人上午的工作时间和加工的零件数,点 的横、纵坐标分别为第 名工人下午的工作时间和加工的零件数, .
①记 为第 名工人在这一天中加工的零件总数,则 , , 中最大的是________.
②记 为第 名工人在这一天中平均每小时加工的零件数,则 , , 中最大的是________.

在 中, , .
(1)求 的值;
(2)若 ,求 的面积.
如图,在四棱锥 中,底面 为正方形,平面 平面 ,点M在线段PB上, 平面 , , .
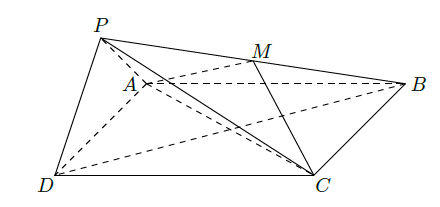
(1)求证:M为PB的中点;
(2)求二面角 的大小;
(3)求直线MC与平面BDP所成角的正弦值.
为了研究一种新药的疗效,选100名患者随机分成两组,每组各 名,一组服药,另一组不服药.一段时间后,记录了两组患者的生理指标 和 的数据,并制成如图,其中“*”表示服药者,“+”表示未服药者.
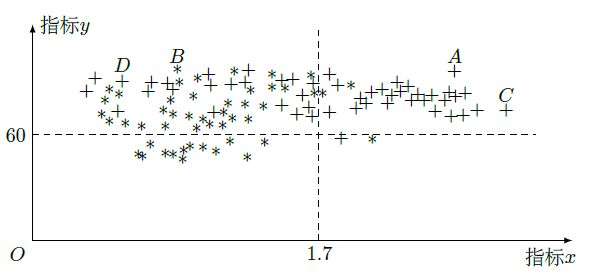
(1)从服药的50名患者中随机选出一人,求此人指标 的值小于 的概率;
(2)从图中A,B,C,D四人中随机选出两人,记 为选出的两人中指标x的值大于1.7的人数,求 的分布列和数学期望 ;
(3)试判断这100名患者中服药者指标 数据的方差与未服药者指标y数据的方差的大小.(只需写出结论)
已知抛物线 过点 .过点 作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP、ON交于点A,B,其中O为原点.
(1)求抛物线C的方程,并求其焦点坐标和准线方程;
(2)求证:A为线段BM的中点.
已知函数 .
(1)求曲线 在点 处的切线方程;
(2)求函数 在区间 上的最大值和最小值.
设 和 是两个等差数列,记 ,其中 表示 , …, 这s个数中最大的数.
(1)若 , ,求 , , 的值,并证明{cn}是等差数列;
(2)证明:或者对任意正数 ,存在正整数 ,当 时, ;或者存在正整数 ,使得 , , , …是等差数列.