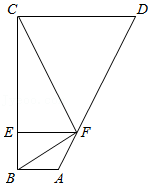
某同学的作业如下框,其中※处填的依据是
如图,已知直线 , , , .若 ,则 . 请完成下面的说理过程. 解:已知 , 根据 内错角相等,两直线平行 ,得 . 再根据(※),得 . |

| A. |
两直线平行,内错角相等 |
B. |
内错角相等,两直线平行 |
| C. |
两直线平行,同位角相等 |
D. |
两直线平行,同旁内角互补 |
如图,将一副三角尺按图中所示位置摆放,点 在 上,其中 , , , , ,则 的度数是

| A. |
|
B. |
|
C. |
|
D. |
|
将一把直尺和一块含 和 角的三角板 按如图所示的位置放置,如果 ,那么 的大小为

| A. |
|
B. |
|
C. |
|
D. |
|
如图,直线 , 的顶点 在 上,若 ,则

| A. |
|
B. |
|
C. |
|
D. |
|
两个直角三角板如图摆放,其中 , , , 与 交于点 .若 ,则 的大小为

| A. |
|
B. |
|
C. |
|
D. |
|
小星在"趣味数学"社团活动中探究了直线交点个数的问题.现有7条不同的直线 ,2,3,4,5,6, ,其中 , ,则他探究这7条直线的交点个数最多是
| A. |
17个 |
B. |
18个 |
C. |
19个 |
D. |
21个 |
如图, ,若 , ,则 的度数为
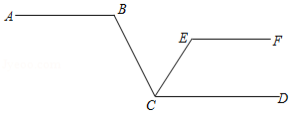
| A. |
|
B. |
|
C. |
|
D. |
|
如图, , ,垂足为 , ,则 等于

| A. |
|
B. |
|
C. |
|
D. |
|
如图,直线 与直线 、 都相交.若 , ,则
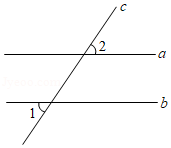
| A. |
|
B. |
|
C. |
|
D. |
|
如图,在 中, , 平分 ,则 的度数为

| A. |
|
B. |
|
C. |
|
D. |
|
已知 的三个顶点都是同一个正方形的顶点, 的平分线与线段 交于点 .若 的一条边长为6,则点 到直线 的距离为 .

如图,在 中,点 、 分别在 、 上, , ,若 ,则 .

如图,已知 , 是 的平分线,若 ,则 .
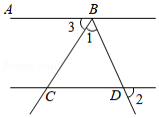
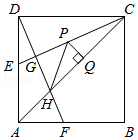
如图,正方形 中, ,连接 , 的平分线交 于点 ,在 上截取 ,连接 ,分别交 , 于点 , ,点 是线段 上的动点, 于点 ,连接 .下列结论:① ;② ;③ ;④ 的最小值是 ,其中正确结论的序号是 .
如图, , ,直线 与 , 的延长线分别交于点 , ,求证: .

如图,点 、 、 、 在同一条直线上, , , .求证: .

如图, 是 的角平分线,在 上取点 ,使 .
(1)求证: ;
(2)若 , ,求 的度数.

如图, 、 、 、 是直线 上的四点, , , .
(1)求证: ;
(2)将 沿直线 翻折得到△ .
①用直尺和圆规在图中作出△ (保留作图痕迹,不要求写作法);
②连接 ,则直线 与 的位置关系是 .

如图,在四边形 中, , , ,点 、 分别在线段 、 上,且 , , .
(1)求证: ;
(2)求证:以 为直径的圆与 相切;
(3)若 , ,求 的面积.