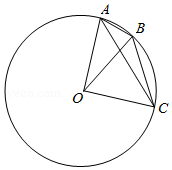
如图, , , 是半径为1的 上的三个点,若 , ,则 的度数为
| A. |
|
B. |
|
C. |
|
D. |
|
如图,从一块直径是2的圆形铁片上剪出一个圆心角为 的扇形,将剪下来的扇形围成一个圆锥.那么这个圆锥的底面圆的半径是

| A. |
|
B. |
|
C. |
|
D. |
1 |
点 是 内一点,过点 的最长弦的长为 ,最短弦的长为 ,则 的长为
| A. |
|
B. |
|
C. |
|
D. |
|
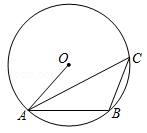
如图, , 是 上直径 两侧的两点,设 ,则
| A. |
|
B. |
|
C. |
|
D. |
|
在 中, ,分别过点 , 作 平分线的垂线,垂足分别为点 , , 的中点是 ,连接 , , .则下列结论错误的是
| A. |
|
B. |
|
C. |
|
D. |
|
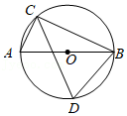
如图,点 , , 是 上的三点.若 , ,则 的大小为
| A. |
|
B. |
|
C. |
|
D. |
|
如图,四边形 内接于 ,点 为边 上任意一点(点 不与点 , 重合)连接 .若 ,则 的度数可能为
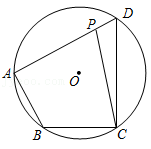
| A. |
|
B. |
|
C. |
|
D. |
|
如图,在 中, , , ,以点 为圆心, 的长为半径画弧,交 于点 ,交 于点 ,以点 为圆心, 的长为半径画弧,交 于点 ,交 于点 ,则图中阴影部分的面积为
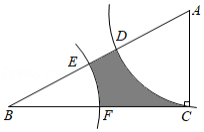
A. B. C. D.
如图,公园内有一个半径为18米的圆形草坪,从 A地走到 B地有观赏路(劣弧 AB)和便民路(线段 AB).已知 A、 B是圆上的点, O为圆心, ,小强从 A走到 B,走便民路比走观赏路少走( )米.
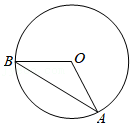
| A. |
|
B. |
|
C. |
|
D. |
|
如图,直角坐标系中,以5为半径的动圆的圆心 沿 轴移动,当 与直线 只有一个公共点时,点 的坐标为
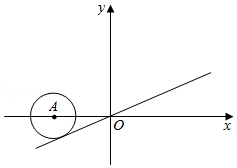
| A. |
|
B. |
|
C. |
|
D. |
|
如图,在 中,弦 的长为4,圆心到弦 的距离为2,则 的度数为 .
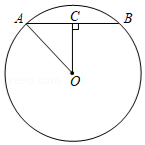
如图,在 内接四边形 中,若 ,则 .
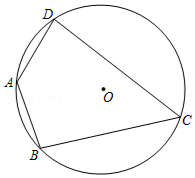
如图,在 中, , , ,点 从点 出发沿 方向运动,到达点 时停止运动,连结 ,点 关于直线 的对称点为 ,连结 , .在运动过程中,点 到直线 距离的最大值是 ;点 到达点 时,线段 扫过的面积为 .

如图所示的扇形中,已知 , , ,则 .
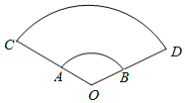
如图,在 中, , , ,以点 为圆心,3为半径的 ,与 交于点 ,过点 作 交 于点 ,点 是边 上的动点,则 的最小值为 .

如图, 、 是 的半径,点 在 上, , ,则 .

如图,圆 的半径为1, 内接于圆 .若 , ,则 .

如图,在 中, ,以 为直径的 与 相切于点 ,连接 .若 ,则 的周长为 .
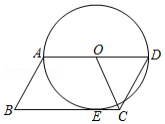
如图,作 的任意一条直径 ,分别以 、 为圆心,以 的长为半径作弧,与 相交于点 、 和 、 ,顺次连接 、 、 、 、 、 ,得到六边形 ,则 的面积与阴影区域的面积的比值为 .

如图,从一块直径为 的圆形铁皮上剪出一个圆心角为 的扇形,则此扇形的面积为 .