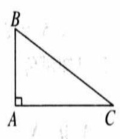图①是第七届国际数学教育大会(ICME)会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图②所示的四边形
.若
,则
的值为( )

| A. |
|
B. |
|
C. |
|
D. |
|
构建几何图形解决代数问题体现了“数形结合”的重要思想.在计算
时,如图所示,在
中,
,延长
使
,连接
,得
,所以
.类比这种方法,计算
的值为( )

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在矩形
中,
的半径为1.现将一个直角三角板的直角顶点与矩形的对称中心
重合,绕着
点转动三角板,使它的一条直角边与
切于点
,此时两直角边与
交于
两点,则
的值为( )

| A. |
|
B. |
|
C. |
|
D. |
|
在直角
中,
为直角,
的平分线
交
于点
边的中点为
,且
,则
( )
| A. |
|
B. |
|
C. |
|
D. |
|
如图,点
是双曲线
上一点,过
作
轴,交直线
于点
,点
是
轴上一点,连接
交双曲线于点
,连接
,若
的面积为
,则
的值为( )

| A. |
|
B. |
|
C. |
|
D. |
|
在
中,
分别为角
的对边,若
,则
的值为 ( )
已知锐角
中,设
,则
的大小关系为( )
| A. |
|
B. |
|
C. |
|
D. |
无法确定
|
已知
,且
,则
的值为( )
| A. |
|
B. |
|
C. |
|
D. |
|
如图, 已知正方形
的边长为
,
为
边上一点, 以点 D为中心,将
按逆时针方向旋转得
,连接
,分别交
于点
.若
,则
_____.

若
,则
的值为_____.
如图,在菱形
中,
为垂足,若
是
边上的一个动点,则线段
长度的最小值是_____.

如图,已知
是矩形
的对角线
上一动点,正方形
的顶点
分别在边
上,若
,则
的值为_____.

如图,在平行四边形
中,
.过点
作
,垂足为
,则
_____.

如图,等腰
中,
,以
为直径作
交
于点
,交
于点
,垂足为
,交
的延长线于点
,则
_____.

已知
中,满足
,
,则
_____.
已知
为锐角,且
,则
_____.
如图,在
中,
,作
的垂直平分线交
于点
,延长
至点
,使
.
(1)若
,求
的周长;
(2)若
,求
的值.
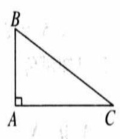
如图,已知
中,
是
的中点,
,求
的值.

如图,
是
的直径,
是
上两点,
是
的中点,过点
作
的垂线,垂足为
,连接
交
于点
.
(1)求证:
是
的切线;
(2)若
,求
的值.

已知
的一边 AC 为关于
的一元二次方程
的两个正整数根之一,且另两边长为
,求
的值.
在
中,
分别是
的对边,且
,若关于
的方程
有两个相等的实数根,又方程
的两实数根的平方和为
,求
的面积.
如图,在
中,
为
上一点,
.
(1)求
的长;
(2)利用此图,求
的精确值.

如图,矩形
的对角线
相交于点
,过点
作
交
于点
,若
的面积为
,求
的值.