已知方程组 的解满足方程 ,则 ( )
| A. |
|
B. |
|
C. |
|
D. |
|
若 ,且 ,则 的值为( )
| A. |
|
B. |
|
C. |
|
D. |
|
对于任意实数 ,定义运算 ,其中 为常数,符号右边的运算是通常意义的加、乘运算,现已知 ,且 ,则 的值为( )
| A. |
|
B. |
|
C. |
|
D. |
|
若 ,则代数式 的值等于( )
| A. |
|
B. |
|
C. |
|
D. |
|
如图,利用两个长方体木块测量一张桌子的高度,首先按图①方式放置,再交换两木块的位置,按图②方式放置.测量的数据如图,则桌子的高度是( )
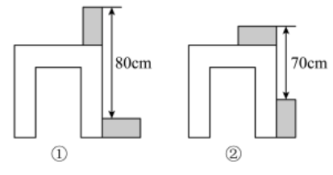
| A. |
|
B. |
|
C. |
|
D. |
|
将 ,这 个整数分为两组,使得一组中所有数的和比另一组中所有数的和大 ,这样的分组方法( )
| A. |
只有一种 |
B. |
恰有两种 |
C. |
多于三种 |
D. |
不存在 |
若方程组 与 有公共解,则 的值为_____.
已知对任意的有理数 ,关于 的二元一次方程 有一组公共解,则公共解为_____.
已知 ,的值只能取 中的一个,且 , ,那么 _____.
某人步行 ,先沿平坦道路走,然后上山,再沿来的路线返回,若在平坦道路上每小时走 ,上山每小时走 ,下山每小时 ,那么 共走了_____路程.
如图,长方形 中,放置 个形状、大小都相同的小长方形,则图中阴影部分的面积为_____.

小王沿街匀速行走,发现每隔 从背后驶过一辆18路公交车,每隔 迎面驶来一辆18路公交车,假设每辆18路公交车行驶速度相同,而且18路公交车总站每隔固定时间发一辆车,那么发车间隔的时间是_____ .
为何值时,方程组
(1)有唯一一组解;
(2)无解;
(3)有无穷多组解.
解下列方程组
(1)
(2)
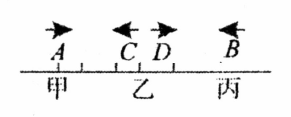
如图,乙地是甲、丙两地的中点, 从甲地, 从丙地, 从乙地分别沿图示的方向同时出发.若 出发后 时遇到 时遇到 时追上 .求 出发后多久遇到 ?多久追上 ?
某班参加一次智力竞赛,共 三题,每题或者得满分或者得零分,其中题 满分 分,题 ,题 满分分别为 分.竞赛结果,每个学生至少答对了一题,三题全答对的有 人,答对其中两道题的有 人,答对题 的人数与答对题 的人数之和为 人,答对题 的人数与答对题 的人数之和为 ,答对题 的人数与答对题 的人数之和为 .问这个班的平均成绩是多少分?
某果品商店进行组合销售,甲种搭配: 水果, 水果;乙种搭配: 水果, 水果, 水果;丙种搭配: 水果, 水果, 水果.已知 水果 元 水果 元 水果 元 .某天该商店销售这三种搭配水果共 元,其中 水果的销售额为 元,问 水果的销售额为多少元?