设 ,对于函数
,对于函数 ,下列结论正确的是 ( )
,下列结论正确的是 ( )
| A.有最大值而无最小值 | B.有最小值而无最大值 |
| C.有最大值且有最小值 | D.既无最大值又无最小值 |
函数y = 1+cos2x的图象 ( )
| A.关于原点对称 | B.关于y轴对称,且有对称中心( ,1) ,1) |
C.关于直线x = 对称 对称 |
D.关于y轴对称,且有对称中心( , , ) ) |
已知函数 在区间
在区间 上的
上的 最小值是
最小值是
 ,则
,则 的最小值等
的最小值等
于( )
A. |
B. |
C.2 | D.3 |
已知函数
 ,且
,且 ,则
,则
的值为 ( )
A.2005 |
B.2006 | C.2007 | D.2008 |
已知函数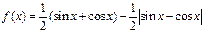 ,则
,则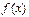 的值域是 ( )
的值域是 ( )
A. |
B.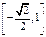 |
C.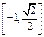 |
D.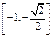 |
若f (sinx)=3-cos2x,则f (cosx)= ( )
| A.3-cos2x | B.3-sin2x | C.3 + cos2x | D.3 + sin2x |
tan 和tan(
和tan( -
- )是方程x2+px+q=0的两根,则
)是方程x2+px+q=0的两根,则 p、q之间的关系是 ( )
p、q之间的关系是 ( )
A.p+q+1="0"  |
B.p-q-1= 0 0 |
C.p+q-1="0" | D.p-q+1="0" |
在 中,角
中,角 所对的边分别是
所对的边分别是 ,若
,若
 ,则
,则
是( )
| A.直角三角形 | B.等边三角形 | C.钝角三角形 | D.等腰角三角形 |
下列函 数中,图象的一部分如右图所示的是 ( )
数中,图象的一部分如右图所示的是 ( )
A. |
B. |
C. |
D. |
若 的内角
的内角 满足
满足 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
已知函数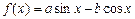 (
(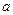 、
、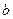 为常数,
为常数,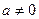 ,
,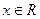 )在
)在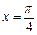 处取
处取
得最小值,则函数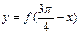 是 ( )
是 ( )
A.偶函数且它的图象关于点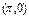 对称 对称 |
B.偶函数且它的图象关于点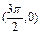 对称 对称 |
C.奇函数且它的图象关于点 对称 对称 |
D.奇函数且它的图象关于点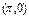 对称 对称 |
若 ,
, ,
, ,则
,则 的值等于( )
的值等于( )
A. |
B. |
C. |
D. |
若 是偶函数,则有序实数对(
是偶函数,则有序实数对( )可以
)可以
是 .
 ,则
,则
 .
.
设函数 .若
.若 是奇函数,则
是奇函数,则 __________.
__________.
已知

 ,s
,s in(
in( )=-
)=- sin
sin 则cos
则cos =________.
=________.
已知 ,
,
(1)求 的值;
的值;
(2)求 的值.
的值.
已知函数 (其中
(其中
 )
)
(1)求函数 的值域;
的值域;
(2)若函数 的图象与直线
的图象与直线 的两个相邻交点间的距离为
的两个相邻交点间的距离为 ,求函数
,求函数 的单调增区间.
的单调增区间.
已知函数f(x)=A (A>0,
(A>0,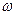 >0,0<
>0,0<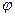 <
<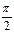 ,且y=f(x)的最大值为2,其
,且y=f(x)的最大值为2,其
图象相邻两对称轴间的距离为2,并过点(1,2).
(1)求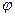 ;
;
(2)计算f (1) + f (2) +… + f ( 2 008 ).
求实数 的取值范围,使不等式
的取值范围,使不等式 恒成立.
恒成立.
如图,已知△ABC是边长为1的正三角形,M、N分别是边AB、AC上的点, 线段MN经过△ABC的中心G,设Ð MGA=a(
MGA=a( ).
).

(1)试将△AGM、△AGN的面积(分别记为S1与S2)表示为a的函数;
(2)求y= 的最大值与最小值.
的最大值与最小值.
已知直线 经过点
经过点 ,
, 且与
且与 轴的正半轴交于
轴的正半轴交于 两点,求
两点,求 取
取
最小值时直线 的方程.
的方程.