下列指定的对象，不能构成集合的是
| A．一年中有31天的月份 |
B．平面上到点 的距离等于1的点 |
C．满足方程 的 |
| D．某校高一（1）班性格开朗的女生 |
函数
的定义域为
A． |
B． |
C． R |
D． |
下列三个图象中，能表示y是x的函数图象的个数是
| A．0 | B．1 | C．2 | D．3 |
下列函数中为偶函数的是
A． |
B． |
C． |
D． |
函数f(x)=7+ax-3 (a>0,a≠1)的图象恒过定点P，则定点P的坐标为
| A．(3,3) | B．(3,2) | C．(3,8) | D．(3,7) |
，
，
的大小关系为
A． |
B． |
C． |
D． |
f(x)是定义在R上的减函数,则不等式
的解集为
| A．(0 ,+∞) | B．(0 , 2) | C．(2 ,+∞) | D．(-∞，2) |
若集合 {0，a2，a+b}={1，a，
}，则a2012 + b2011的值为
| A．0 | B．1 | C．-1 | D．±1 |
设函数
，则
的表达式是
A． |
B． |
C． |
D． |
已知函数
（其中
）的图象如下面右图所示，则函数
的图象是
根据表格中的数据，可以断定方程
(
０)的一个根所在的区间是
 |
－1 |
0 |
1 |
2 |
3 |
 |
0.37 |
1 |
2.70 |
7.29 |
19.68 |
 |
2 |
4 |
6 |
8 |
10 |
A．（－1，0） B．（0，1） C．（1，2） D．（2，3）
设映射
是集合
到集合
的映射，若对于实数
，在
中不存在对应的元素，则实数
的取值范围是
A．
B．
Ｃ．
D．
已知全集
函数y＝－(x－2)x的递增区间是____________，递减区间是
已知
，若
，则
已知f（x）是定义在
∪
上的奇函数，当
时，f（x）的图象如右图所示，那么f（x）的值域是 
计算：
（1)
（2）
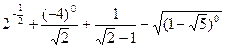
已知
，
.
（1）求
和
；
（2）若记符号
，
在图中把表示“集合
”的部分用阴影涂黑，求
．
已知函数
.
（I）判断函数
的奇偶性并证明；
（II）若
，证明：函数在区间
上是增函数.
已知函数
.
（1）当
时，求函数f(x)
的最大值和最小值；
（2）求实数
的取值范围，使
在区间
上是单调函数
某微机培训机构打算购进一批微机桌和鼠标垫
，市场价微机桌每张为150元，鼠标垫每个为５元，该培训机构老板联系了两家商场甲和乙，由于用货量大，这
两家商场都给出了优惠条件
商场甲：买一赠一，买一张微机桌，赠一个鼠标垫
商场乙：打折，按总价的95%收款
该培训机构需要微机桌
60张，鼠标垫
个（
），如果两种商品只能在一家购买，请你帮助该培训机构老板选择在哪一家商场买更省钱？
已知指数函数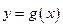
满足：g(3)=8，定义域为
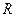的函数
是奇函数.
（1）确定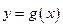的解析式；
（2）求m，n的值；
（3）若对任意的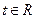
，不等式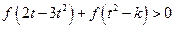
恒成立，求实数
的取值范围